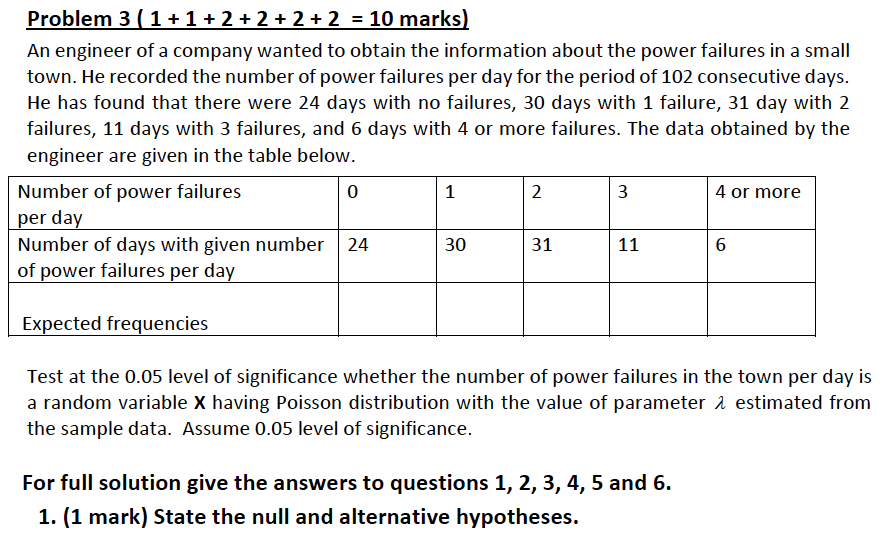
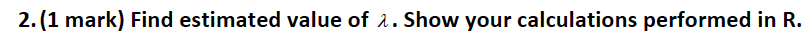
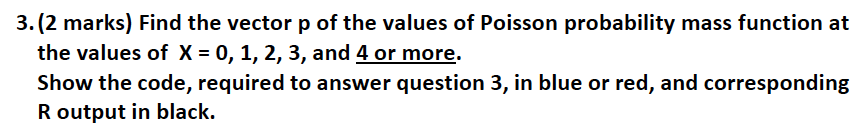
Problem 3 (1 + 1 + 2 + 2 + 2+ 2 = 10 marks) An engineer of a company wanted to obtain the information about the power failures in a small town. He recorded the number of power failures per day for the period of 102 consecutive days. He has found that there were 24 days with no failures, 30 days with 1 failure, 31 day with 2 failures, 11 days with 3 failures, and 6 days with 4 or more failures. The data obtained by the engineer are given in the table below. Number of power failures 0 1 2 3 4 or more per day Number of days with given number 24 30 31 11 6 of power failures per day Expected frequencies Test at the 0.05 level of significance whether the number of power failures in the town per day is a random variable X having Poisson distribution with the value of parameter 1 estimated from the sample data. Assume 0.05 level of significance. For full solution give the answers to questions 1, 2, 3, 4, 5 and 6. 1. (1 mark) State the null and alternative hypotheses.2. (1 mark) Find estimated value of 2. Show your calculations performed in R.3. (2 marks) Find the vector p of the values of Poisson probability mass function at the values of X = U, 1, 2, 3, and 4 or more. Show the code, required to answer question 3, in blue or red, and corresponding R output in black. 4. (2 marks) Find expected frequencies at the values of X = 0, 1, 2, 3, and 4 or more. Check whether all expected frequencies are no less than 5, and there is no need to combine the cells. Show the code, required to answer question 4, in blue or red, and corresponding R output in black. 5. (2 marks) Perform chi - square test and represent its results. Show the code, required to answer question 5, in blue or red, and corresponding R output in black. 6. (2 marks) Make the conclusions about truth or falsity of stated hypotheses. Decide whether the data indicate that the number of power failures in the town per day is a random variable X having Poisson distribution with the value of parameter A estimated from the sample data