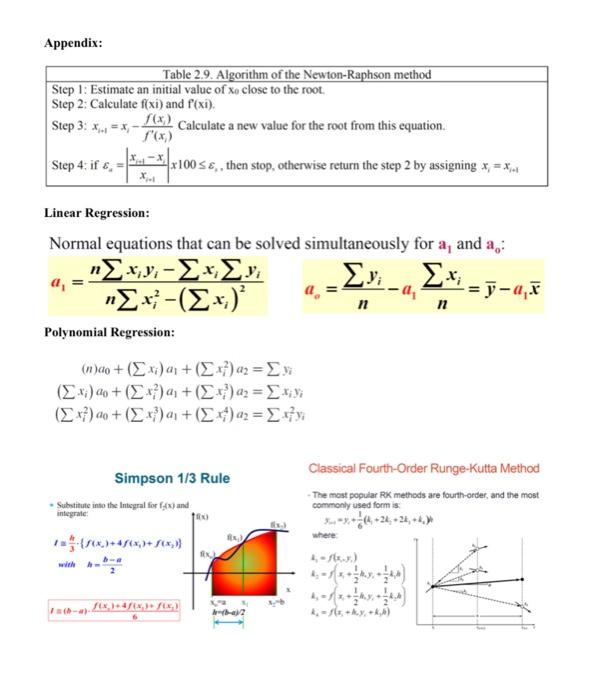
Problem 3 (20 pts): Solve the following differential equations using the fourth order Runge-Kutta method. For x=0, assume y1=4 and y2=6. Integrate up to x=0.5 by taking the step size 0.5. dxdy1=0.5y1dxdy2=40.3y20.1y1 (Correct solution set up is 5pts and correct results are 15pts ) Appendix: \begin{tabular}{l} Table 2.9. Algorithm of the Newton-Raphson method \\ \hline Step 1: Estimate an initial value of x0 close to the root. \\ Step 2; Calculate f(x) and f(xi). \\ Step 3: xi+1=xif(xi)f(xi) Calculate a new value for the root from this equation. \\ Step 4: if a=xi+1xi+1xjx100,, then stop, otherwise return the step 2 by assigning xi=xi+1 \\ \hline \end{tabular} Linear Regression: Normal equations that can be solved simultaneously for a1 and a0 : a1=nxi2(xi)2nxiyixiyiao=nyia1nxi=ya1x Polynomial Regression: (n)a0+(xi)a1+(xi2)a2(xi)a0+(xi2)a1+(xi3)a2(xi2)a0+(xi3)a1+(xi4)a2=yi=xiyi=xi2yi Simpson 1/3 Rule Classical Fourth-Order Runge-Kutta Method - The most popular RX methods are fourth-order, and the most - Subtitute into the Intsyral for ff(x) and commonly used form is. integrale: f=3h{f(xn)+4f(x1)+f(x2)}withh=2ba 1,f(x,y)i2=f(x+21knx1+21k1,k)