Problem 3. (30 points, 2 each part) Answer this problem on this sheet using the spaces indicated.

Answer the following questions regarding the following primal model using the solution and analysis of

sensitivity obtained with Excel Solver which is on the next page.

X1 = Number of apple trees to plant

X2 = Number of avocado trees to plant

Max Z = 5000X1 + 7000X2 (Total profit)

subject to

20X1 + 10X2  1000 (Fertilizer available in Ton)

2X1 + 3X2  200 (Hectares of land available)

X1 + 2X2  2400 (Available man hours)

25X1 + 50X2  35000 (Liters of water available)

10X1 + 15X2  15000 (Budget available)

X1, X2  0

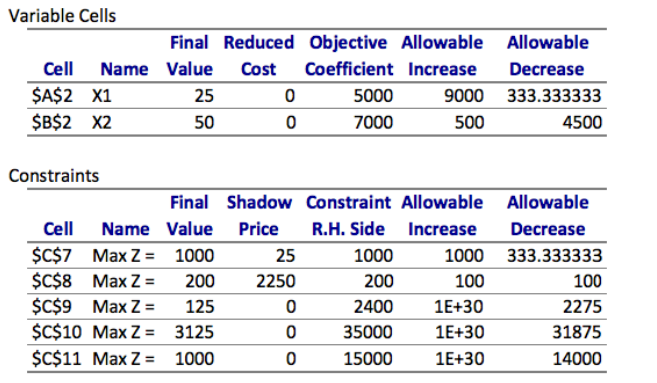
8. If the number of hectares is reduced to 199, the optimal total utility is _______________________________.

9. If the number of liters of water is doubled (from 35,000 to 70,000, the optimal total utility is _______________.

10. Company workers want to work overtime. How much would be the maximum that the company would be

willing to pay for every extra hour? __________________________________________________.

11. Why is the shadow price of the fourth restriction (liters of water available) 0? ____________________

___________________________________________________________________________________________

_________________________________________________________________________________

12. If we increase the number of hectares available from 200 to 300, the optimal total utility is ____________.

13. If the profit for each avocado tree changes from 7000 to 7100, do the optimal values of the variables of

X1 and X2? _______. If yes, what are the new values of X1 and X2? __________.

14. If the profit for each avocado tree changes from 7000 to 7100, does the optimal value of the objective function change?

_______. If yes, what is the new value of Z? _______________.

15. The company is offered 100 tons of fertilizer at 50 per ton. Should you buy them? ____________

Answer must be obtained withouth any software

Problema 3. (30 puntos, 2 cada inciso) Conteste este problema en esta hoja utilizando los espacios indicados. Contestar las siguientes preguntas con respecto al siguiente modelo primal utilizando la solucin y anlisis de sensibilidad obtenidos con Solver de Excel la cual est en la siguiente pgina. X1 = Nmero de rboles de manzana a plantar X2 = Nmero de rboles de aguacate a plantar (Utilidad total) Max Z= 5000X1 + 7000X2 sujeto a 20X1 + 10X2 0 (Fertilizante disponible en Ton) (Hectreas de tierra disponibles) (Horas hombre disponibles) (Litros de agua disponibles) (Presupuesto disponible) Variable Cells Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient Increase Decrease $A$2 X1 25 0 5000 9000 333.333333 $B$2 X2 50 0 7000 500 4500 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $C$7 Max 2 = 1000 25 1000 1000 333.333333 $C$8 Max Z= 200 2250 200 100 100 $C$9 Max 2 = 125 0 2400 1E+30 2275 $C$10 Max 2 = 3125 0 35000 1E+30 31875 $C$11 Max 2 = 1000 0 15000 1E+30 14000