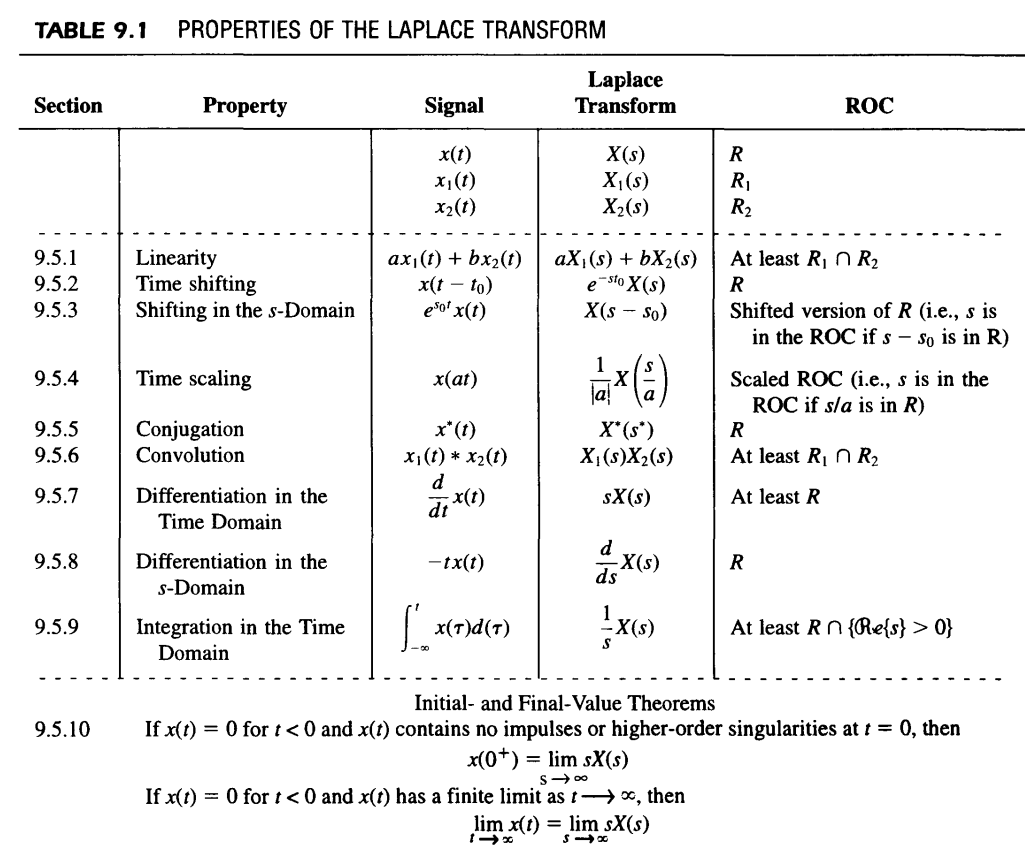
Problem 3 [5 points] (Laplace transform) A linear time-invariant (LTI) system has input x(t), impulse response h(t), and output y(t). Assume that the input is given by: x(t) = eu(t) where u(t) is the unit step function. Regarding the impulse response, we know that h(t) is causal and BIBO stable, and its Laplace transform is given by: H(s) = = 8+5 i) [2 points] Calculate the Laplace transform X(s) and its region of convergence (ROC). ii) [1 point] Find the ROC of H(s), and calculate h(t). iii) [1 point] Suppose that the ROC of H(s) is Re{s} > 5. Calculate Y(s) and its ROC. iv) [1 point] Calculate y(t). Note: You can use the properties of the Laplace transform and transformation pairs listed in the Tables 9.1 and 9.2 of the book. TABLE 9.1 PROPERTIES OF THE LAPLACE TRANSFORM Section Property Laplace Transform Signal ROC x(t) X(s) R x(t) X(s) R x2(t) X2(s) R 9.5.1 Linearity ax(t) + bx2(t) 9.5.2 Time shifting x(t - to) ax(s) + bx2(s) e-sto X(s) R 9.5.3 Shifting in the s-Domain eso x(t) X(s - So) 9.5.4 Time scaling x(at) 9.5.5 Conjugation x*(t) X*(s*) R 9.5.6 Convolution x(1) * x2(t) X(s)X2(s) () At least R R Shifted version of R (i.e., s is in the ROC if s - so is in R) Scaled ROC (i.e., s is in the ROC if s/a is in R) At least R R d 9.5.7 Differentiation in the x(t) SX(s) At least R dt Time Domain d 9.5.8 Differentiation in the -tx(t) X(s) R ds s-Domain 9.5.9 Integration in the Time |__ X(T)d(T) 1X(s) At least Rn {Re{s} > 0} S Domain 9.5.10 Initial and Final-Value Theorems If x(t) = 0 for t