PROBLEM 3: Consider the C++ function below:

void fubar(unsigned int n) {

int i, j;

for(i=0; i

cout

}

for(i=0; i

for(j=0; j

cout

}

}

}

3.A: Complete the following table indicating how many ticks are printed for various parameters n.

Unenforceable rule: derive your answers by hand -- not simply by writing a program calling the function.

n	number of ticks printed when fubar(n) is called
0
1
2
3
4

3.B: Derive a closed-form expressing the number of ticks as a function of n -- i.e., complete the following:

For all n0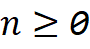, calling fubar(n) results in _____________ ticks being printed

Give a brief justification of your answer; you do not need a formal proof.

PROBLEM 4: Consider the recursive C++ function below:

void foo(unsigned int n) {

if(n==0)

cout

else {

foo(n-1);

foo(n-1);

foo(n-1);

}

}

4.A: Complete the following table indicating how many ticks are printed for various parameters n.

Unenforceable rule: derive your answers by hand -- not simply by writing a program calling the function.

n	number of ticks printed when foo(n) is called
0
1
2
3
4

4.B: Derive a conjecture expressing the number of ticks as a function of n -- i.e., complete the following:

Conjecture: for all n0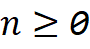, calling foo(n) results in _____________ ticks being printed

4.C: Prove your conjecture from part B (hint: Induction!)