Problem 3: Consider the following linear programming model as the primal model. It is a maximization problem with 1 nonnegative decision variable, denoted by , and three constraints. The sensitivity report of the primal models optimum solution is also given below.

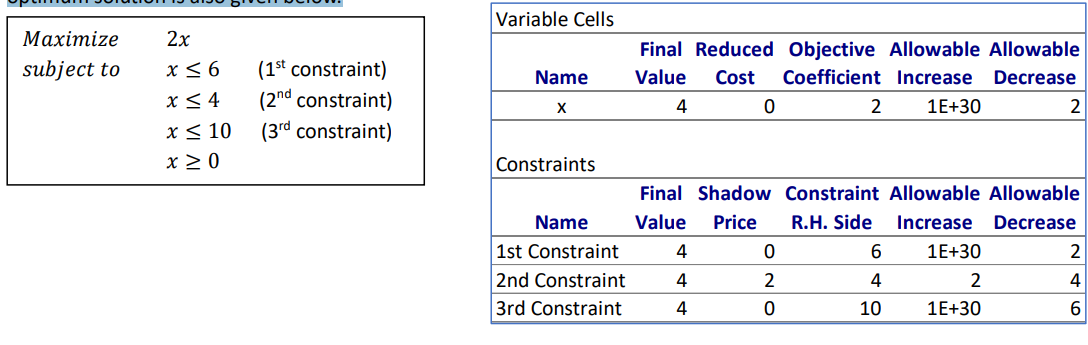
a) Based on the above sensitivity report, what is the optimum solution of the above primal model (select all correct answers):

= 4

= 0

= 2

= 1 + 30 ()

\begin{tabular}{|lll|} \hline Maximize & 2x & \\ subject to & x6 & (1st constraint ) \\ & x4 & (2nd constraint ) \\ & x10 & (3rd constraint ) \\ & x0 & \\ \hline \end{tabular} \begin{tabular}{|c|c|c|c|c|c|} \hline \multicolumn{6}{|l|}{ Variable Cells } \\ \hline Name & FinalValue & ReducedCost & ObjectiveCoefficient & AllowableIncrease & AllowableDecrease \\ \hlinex & 4 & 0 & 2 & 1E+30 & 2 \\ \hline \multicolumn{6}{|l|}{ Constraints } \\ \hline Name & FinalValue & ShadowPrice & ConstraintR.H.Side & AllowableIncrease & AllowableDecrease \\ \hline 1st Constraint & 4 & 0 & 6 & 1E+30 & 2 \\ \hline 2nd Constraint & 4 & 2 & 4 & 2 & 4 \\ \hline 3rd Constraint & 4 & 0 & 10 & 1E+30 & 6 \\ \hline \end{tabular}