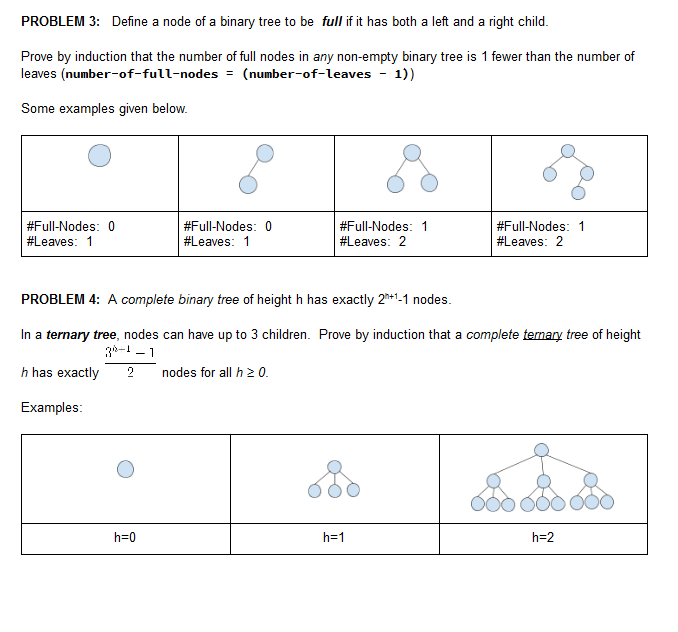
PROBLEM 3: Define a node of a binary tree to be full if it has both a left and a right child. Prove by induction that the number of full nodes in any non-empty binary tree is 1 fewer than the number of leaves (number-of-full-nodes(number-of-leaves - 1)) Some examples given below. .ullAkxles: #Leaves: 1 () #Full-Nodes: #Leaves: 1 0 #Full-Nodes: #Leaves: 2 #Full-Nodes: #Leaves: 2 1 1 PROBLEM 4: A complete binary tree of height h has exactly 2-1 nodes. In a ternary tree, nodes can have up to 3 children. Prove by induction that a complete temary tree of height h has exactly 2nodes for all h 2 0 33-1-1 2 as exactly nodes for all h 0. Examples h=1 h 2