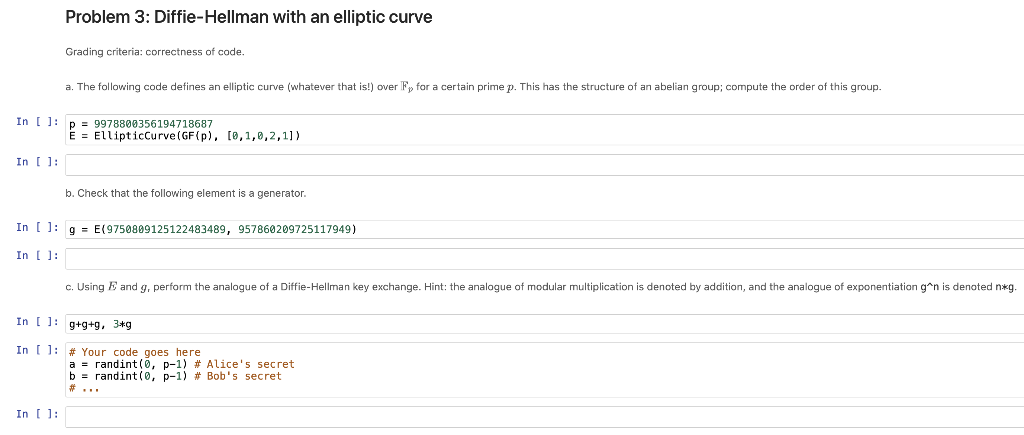
Problem 3: Diffie-Hellman with an elliptic curve Grading criteria: correctness of code. a. The following code defines an elliptic curve (whatever that is!) over Fy for a certain prime p. This has the structure of an abelian group; compute the order of this group. In [ ]: p = 9978800356194718687 E = EllipticCurve (GF(p), [0,1,0,2,1]) In [ ]: b. Check that the following element is a generator. In ]: g = E(9750899125122483489, 957860209725117949) In [ ]: c. Using E and g, perform the analogue of a Diffie-Hellman key exchange. Hint: the analogue of modular multiplication is denoted by addition, and the analogue of exponentiation gan is denoted n*g. In [ ]: 9+9+9, 349 In (): # Your code goes here a = randint(0, P-1) # Alice's secret b = randint(0, P-1) # Bob's secret # ... In [ ]: Problem 3: Diffie-Hellman with an elliptic curve Grading criteria: correctness of code. a. The following code defines an elliptic curve (whatever that is!) over Fy for a certain prime p. This has the structure of an abelian group; compute the order of this group. In [ ]: p = 9978800356194718687 E = EllipticCurve (GF(p), [0,1,0,2,1]) In [ ]: b. Check that the following element is a generator. In ]: g = E(9750899125122483489, 957860209725117949) In [ ]: c. Using E and g, perform the analogue of a Diffie-Hellman key exchange. Hint: the analogue of modular multiplication is denoted by addition, and the analogue of exponentiation gan is denoted n*g. In [ ]: 9+9+9, 349 In (): # Your code goes here a = randint(0, P-1) # Alice's secret b = randint(0, P-1) # Bob's secret # ... In [ ]