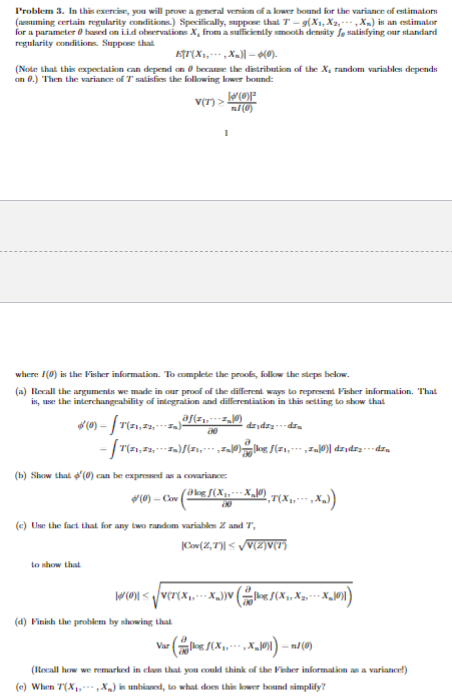
Problem 3. In this exercise, you will prove a general version of a lower bound for the variance of estimators (assuming certain regularity conditions.) Specifically, suppose that T-g(X1, X2, X) is an estimator for a parameter 0 based on Lid observations X, from a sufficiently smooth density fo satisfying our standard regularity conditions. Suppose that ET (X1,---, Xn)] 6(0). (Note that this expectation can depend on 0 because the distribution of the X, random variables depends on 0.) Then the variance of T'satisfies the following lower bound: WOF V(T)> ml(0) where (0) is the Fisher information. To complete the proofs, follow the steps below. (a) Recall the arguments we made in our proof of the different ways to represent Fisher information. That is, use the interchangeability of integration and differentiation in this setting to show that '(0) -|(21,22, ---I) a(1) 20 dzdz dr -(1, 2)/(1-0)|log (#1,---, In|0)| dzidrz --- In (b) Show that '(0) can be expressed as a covariance (0)-C(g(x-XJ0) (e) Use the fact that for any two random variables Z and T, --x)) to show that Cov(Z,T)|V(Z)V(T) (d) Finish the problem by showing that Var (g(x, x 10))-(0) (Recall how we remarked in clan that you could think of the Fisher information as a variance!) (e) When T(X,,X) is unbiased, to what does this lower bound simplify?