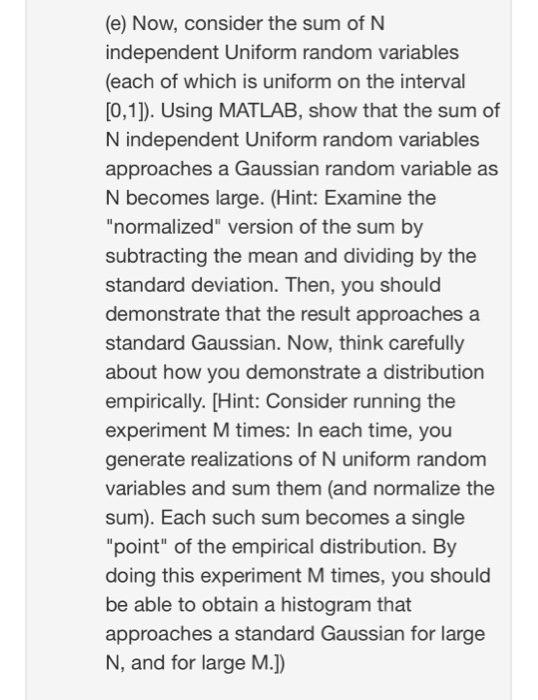
Problem 3: In this problem, you will use the "rand function in MATLAB, which generates a uniform random variable. First, explore this "rand" function in MATLAB and make sure that you understand it. (a) Generate N realizations of a Uniform random variable X on the interval [0,1] in MATLAB. By increasing the number N from 1 to N_max, graph the sample average as a function of N. (You must attach your graph.) (b) To what value does your graph of the sample average converge? What is the empirical value of N_max such that your sample average is within an error of 1% of the expected value of the Uniform random variable? (c) Using Chebyshev's Inequality, compute an upper bound for the probability that the sample average deviates from its expected value by more than 1%. (Hint: You must compute the variance of the Uniform random variable.) [In addition, think about the relationship of Part (c) to Part (b).] (d) State the general result called the Strong Law of Large Numbers". Is the empirical result that you found in (b) in accordance with the Strong Law of Large Numbers? In what sense