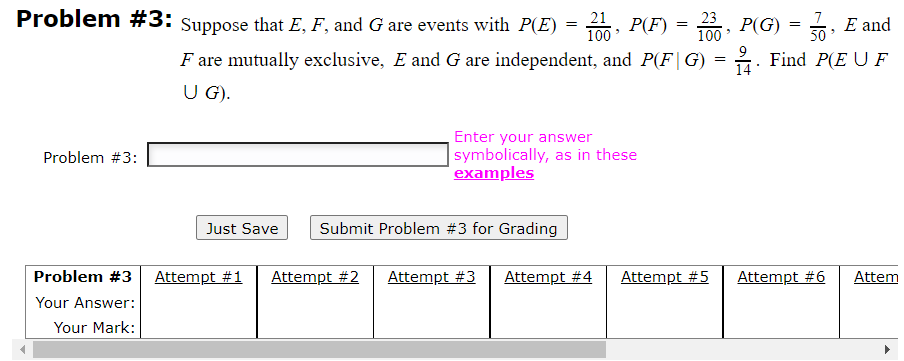
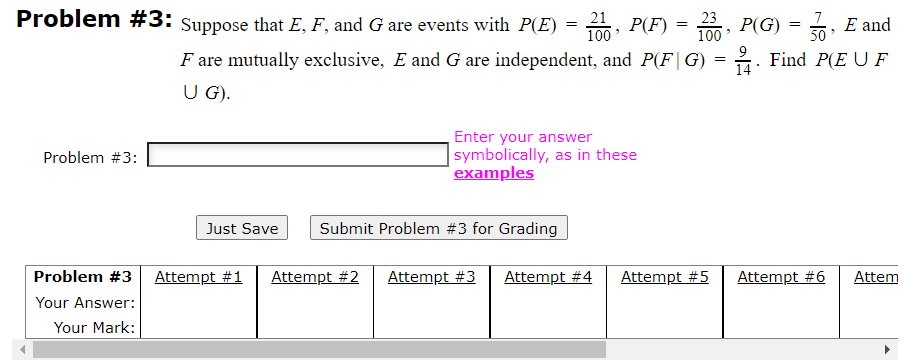
Problem #3: Suppose that E, F, and G are events with P(E) = 21. 100 P(F) = -, P(G) = ~, E and F are mutually exclusive, E and G are independent, and P(F | G) = - 14 . Find P(E U F U G). Enter your answer Problem #3: symbolically, as in these examples Just Save Submit Problem #3 for Grading Problem #3 Attempt #1 Attempt #2 Attempt #3 Attempt #4 Attempt #5 Attempt #6 Attem Your Answer: Your Mark:Problem #7: Suppose that we have 9 coins such that if the ith coin is flipped, heads will appear with probability i/10, i = 1, 2, ...,9. When one of the coins is randomly selected and flipped, it shows tails. What is the conditional probability that it was the 6th coin? Enter your answer Problem #7: symbolically, as in these examples