Problem 3.

Suppose you are a teller and the currency in your country is arranged in coins of increasing C values (each coin has a value of a power of C for some integer C > 1), i.e., you have coins of 1, C, C^(2), ..., C^(k) up to some k >= 1. Your customer wants you to make change for N (N is a positive integer) using the minimum number of coins. Propose an efficient greedy algorithm in pseudocode which returns k +1 numbers 20, 21 : 12... such that (i)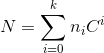 and (ii) the total number of coins used, 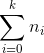, is minimized. Prove that your algorithm is guaranteed to always return the optimal solution, that is, condition (ii) is always satised. (Hint: Prove the two properties, subproblem optimality and substitution property, required for a greedy algorithm to work.)

N = -? niC