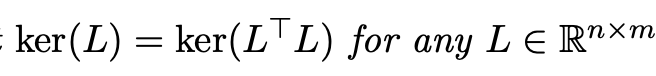
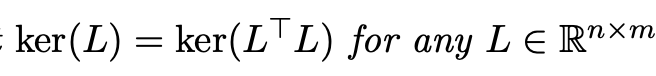
Problem 3.5 (4 points). We will prove, in steps, that rank(L) = rank(LT) for any L E Rnxm. (a) Prove that rank(L) = rank(LTL). (Hint: use Problem 3.4.) (b) Use part (a) to deduce that that rank(L) = rank(LT). ( You may not use the Proposition on slide 7 of Session 3, since that just restates this problem.) ker (L) = ker(L 'L) for any L E Rnxm