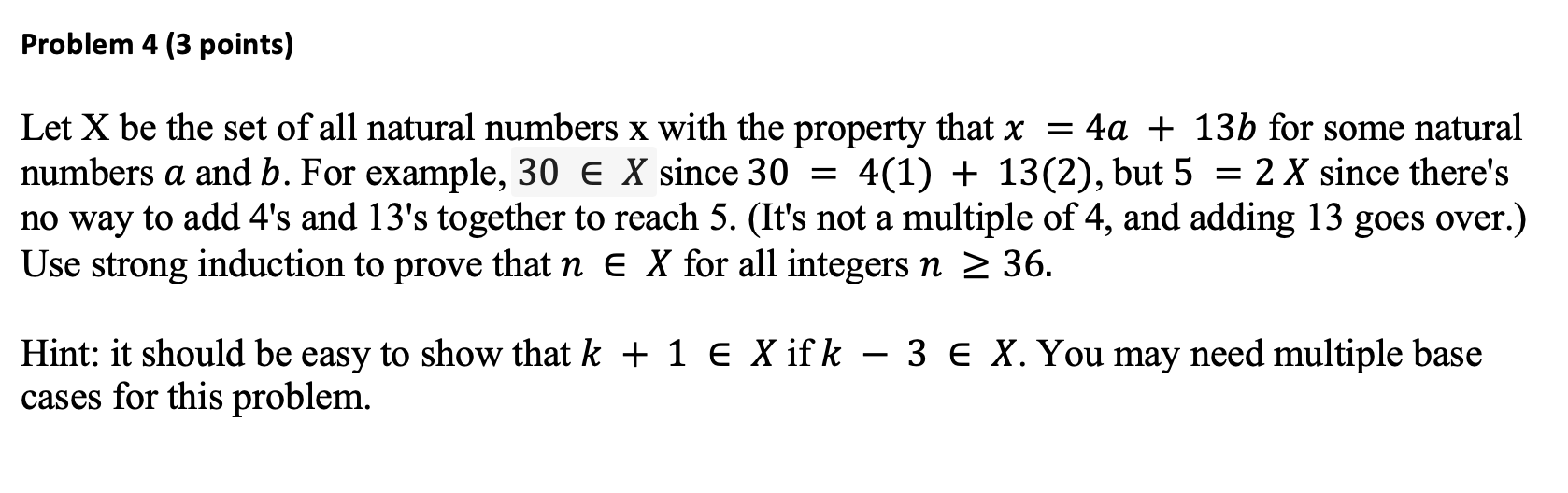
Problem 4 (3 points) Let X be the set of all natural numbers x with the property that x = 4a + 13b for some natural numbers a and b. For example, 30 e X since 30 = 4(1) + 13(2), but 5 = 2 X since there's no way to add 4's and 13's together to reach 5. (It's not a multiple of 4, and adding 13 goes over.) Use strong induction to prove that n e X for all integers n > 36. Hint: it should be easy to show that k + 1 X if k cases for this problem. - 3 E X. You may need multiple base