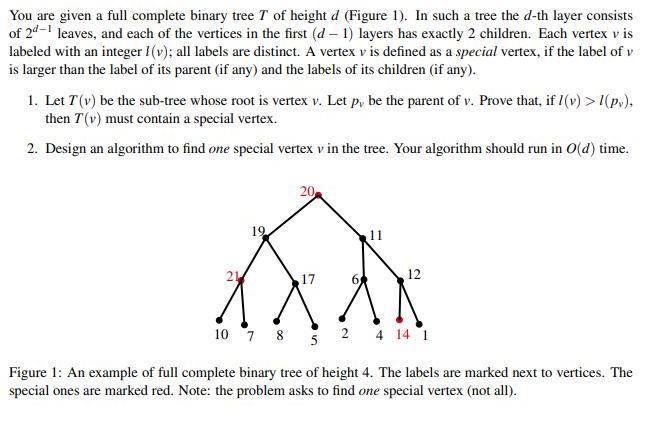
You are given a full complete binary tree T of height d (Figure 1). In such a tree the d-th layer consists of 24-1 leaves, and each of the vertices in the first (d 1) layers has exactly 2 children. Each vertex v is labeled with an integer 1(v); all labels are distinct. A vertex v is defined as a special vertex, if the label of v is larger than the label of its parent (if any) and the labels of its children (if any). 1. Let T(v) be the sub-tree whose root is vertex v. Let p, be the parent of v. Prove that, if I(v) > 1(p,). then T(v) must contain a special vertex. 2. Design an algorithm to find one special vertex v in the tree. Your algorithm should run in O(d) time. 20 19 11 17 12 10 7 8 5 2 4 14 1 Figure 1: An example of full complete binary tree of height 4. The labels are marked next to vertices. The special ones are marked red. Note: the problem asks to find one special vertex (not all).