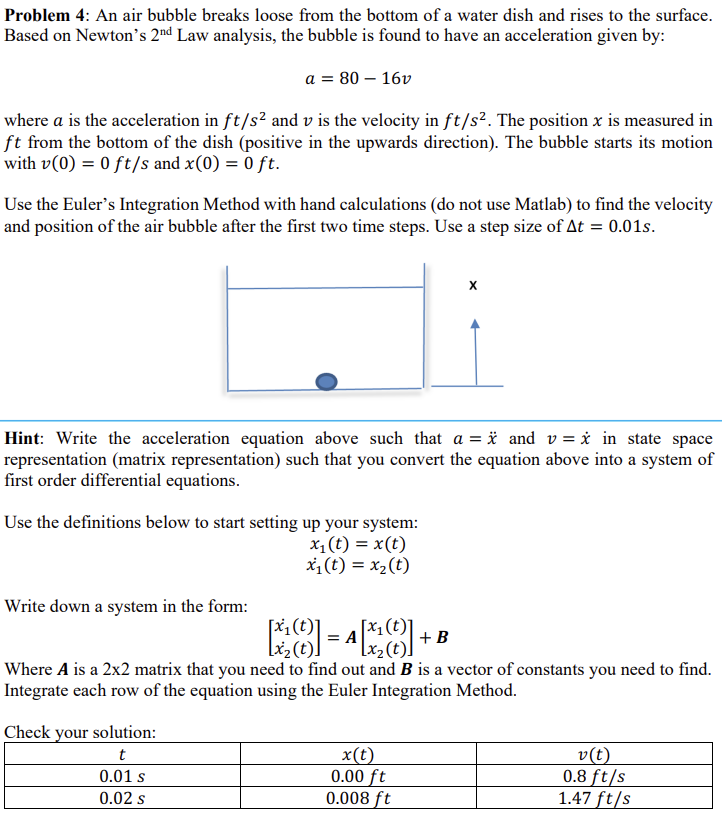
Problem 4: An air bubble breaks loose from the bottom of a water dish and rises to the surface. Based on Newton's 2nd Law analysis, the bubble is found to have an acceleration given by: a = 80 - 16v where a is the acceleration in ft/s and v is the velocity in ft/s. The position x is measured in ft from the bottom of the dish (positive in the upwards direction). The bubble starts its motion with v(0) = 0 ft/s and x(0) = 0 ft. Use the Euler's Integration Method with hand calculations (do not use Matlab) to find the velocity and position of the air bubble after the first two time steps. Use a step size of At = 0.01s. Hint: Write the acceleration equation above such that a = x and v=x in state space representation (matrix representation) such that you convert the equation above into a system of first order differential equations. Use the definitions below to start setting up your system: x(t) = x(t) x(t) = x2(t) Write down a system in the form: [18] = [x(t) A + B Where A is a 2x2 matrix that you need to find out and B is a vector of constants you need to find. Integrate each row of the equation using the Euler Integration Method. Check your solution: t 0.01 s x(t) 0.00 ft v(t) 0.8 ft/s 0.02 s 0.008 ft 1.47 ft/s