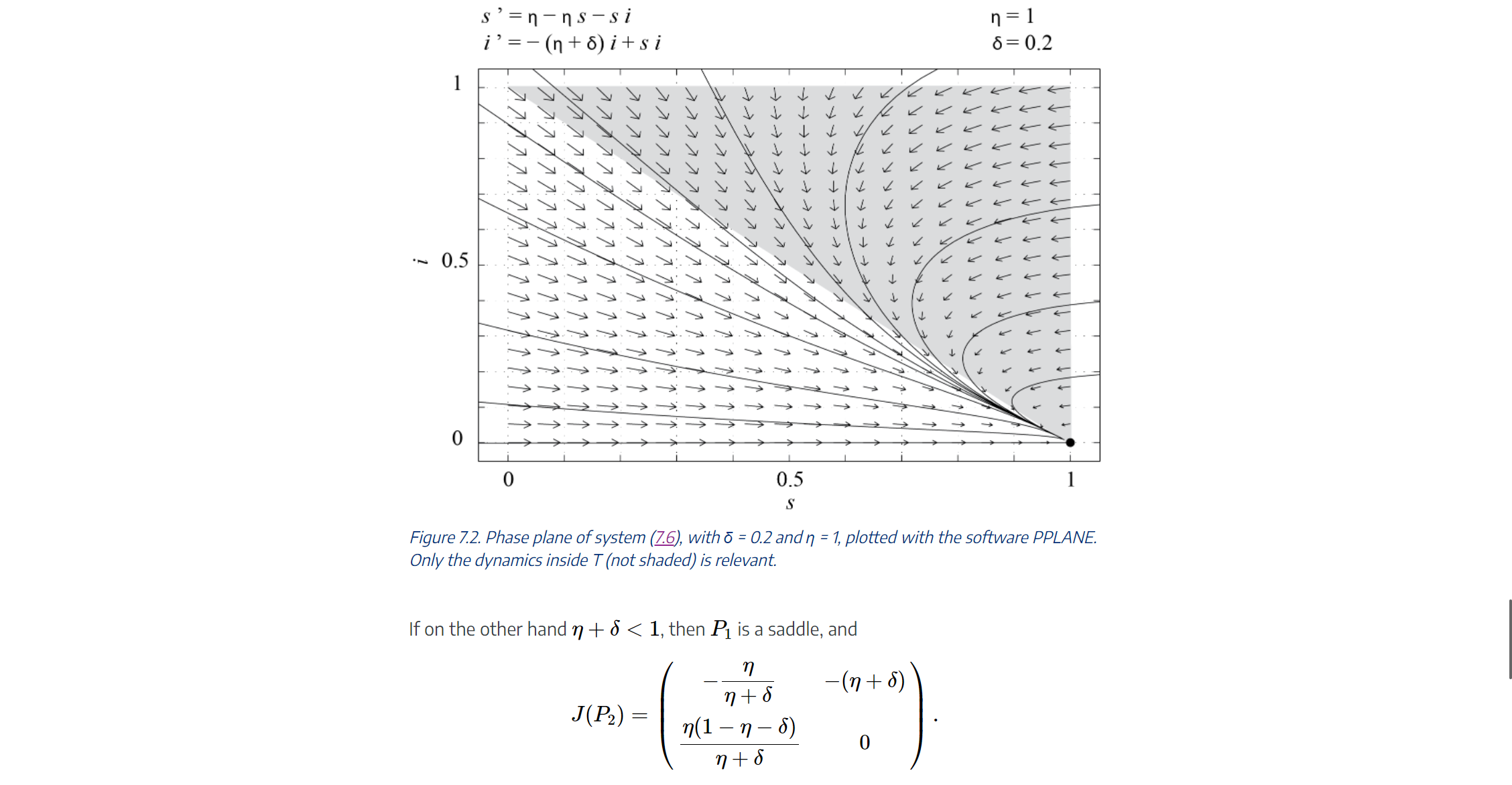
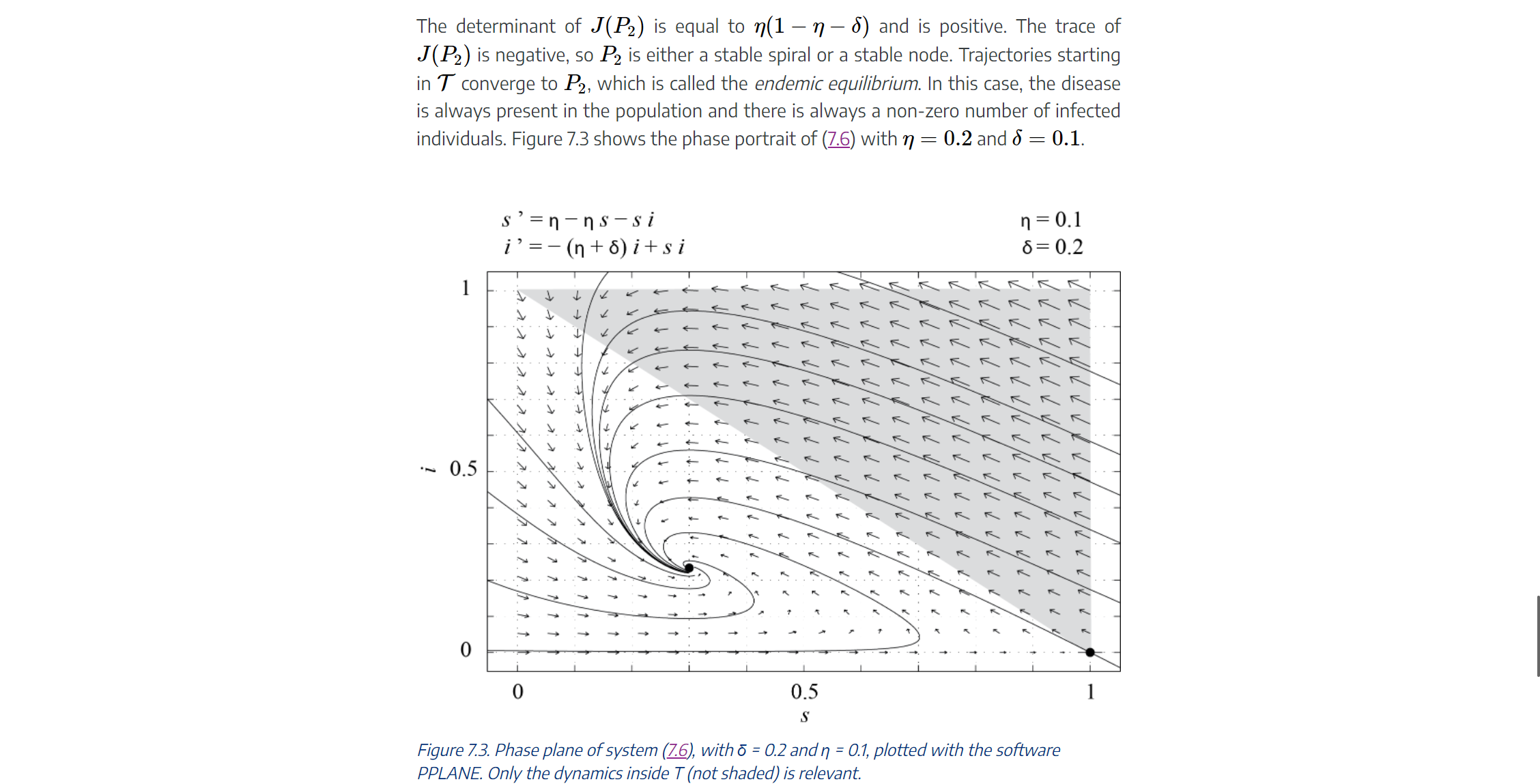
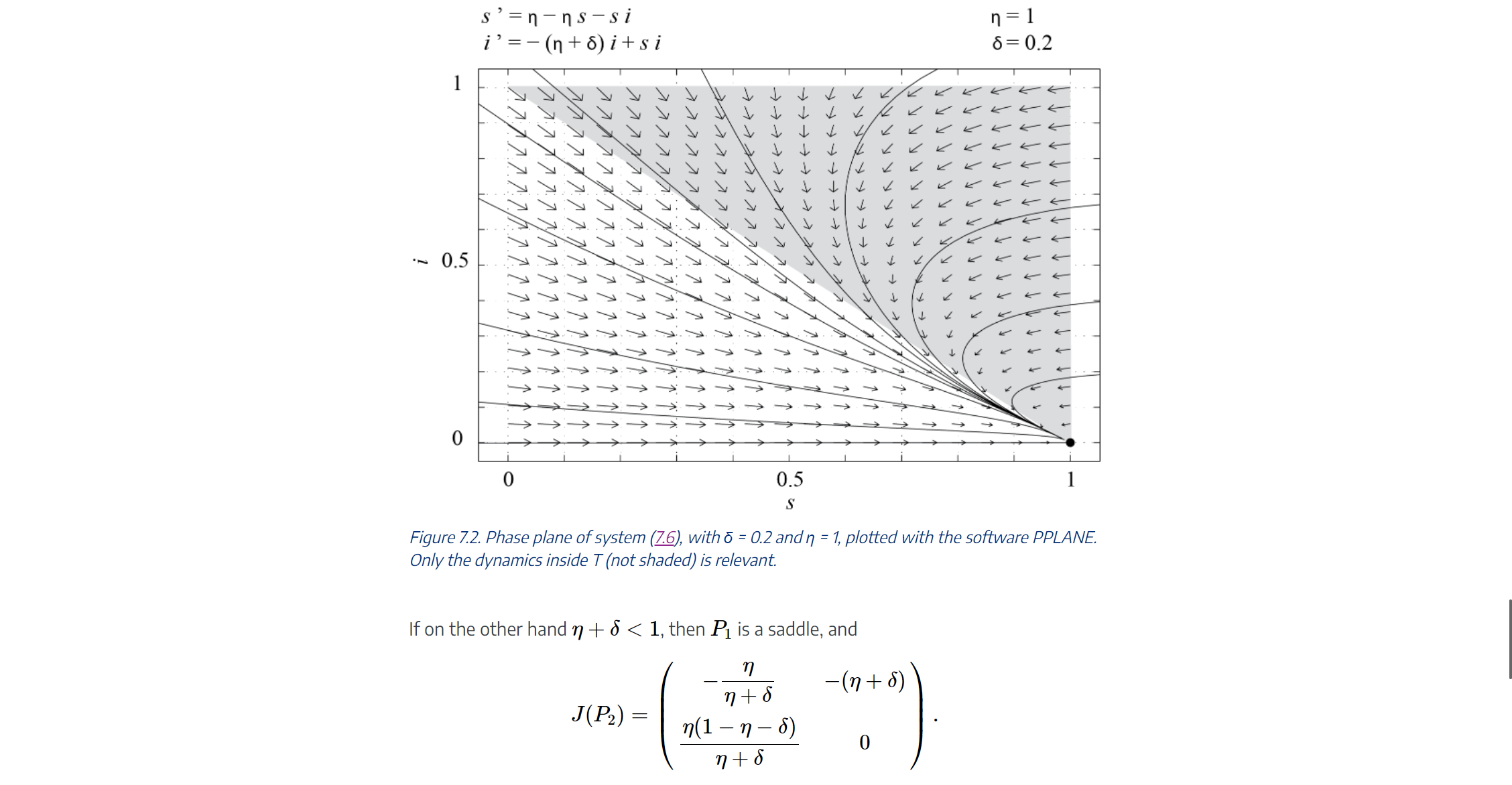
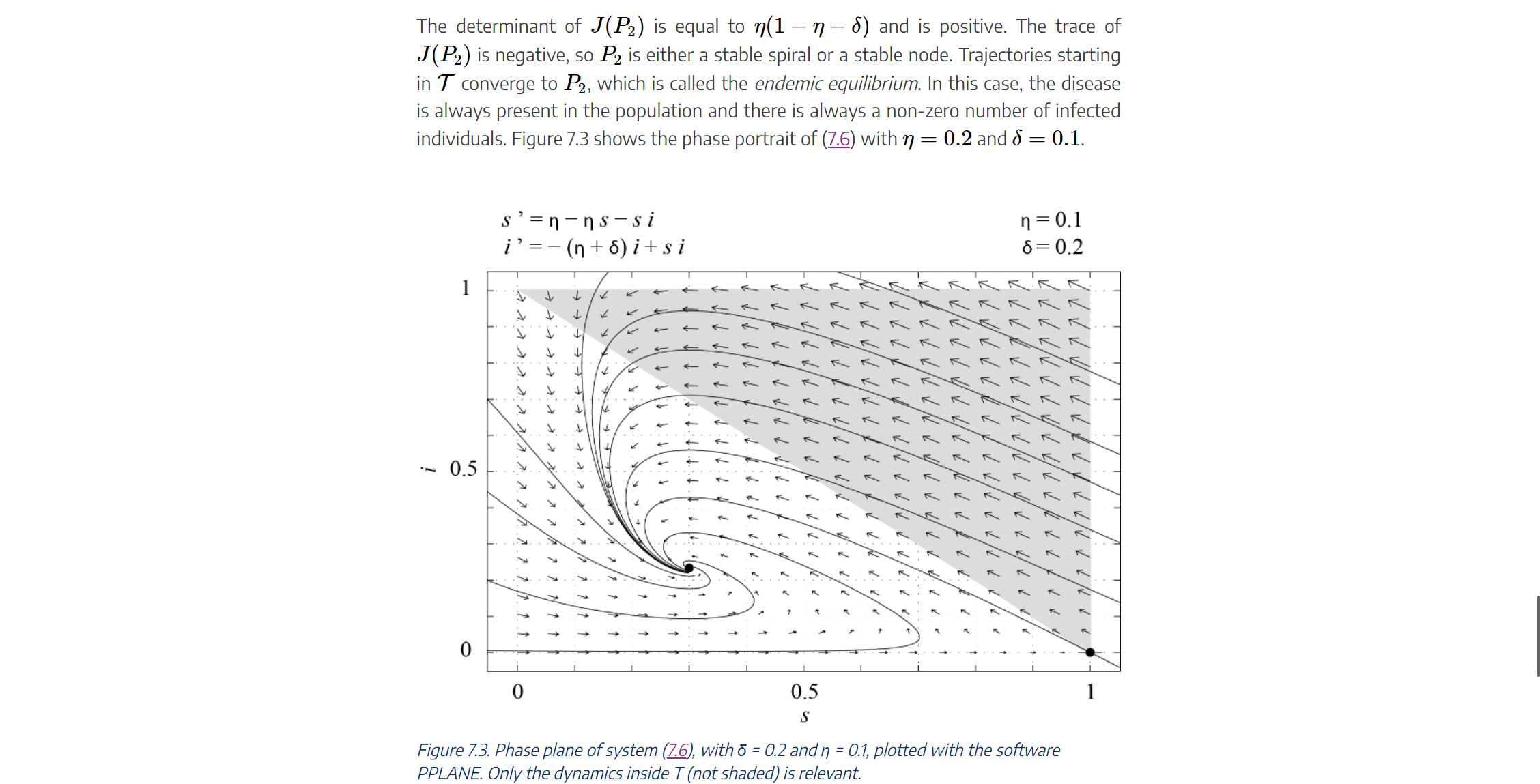
Problem 4 Consider model (7.6) with n + o 0, and R(0) 2 0. Here the new parameters are the per capita death rate / and per capita birth rate v of the pop- ulation. By choosing / = v, the total population N = S + I + R is constant. In this case, using the same dimensionless variables as for the classic SIR model, we are left with a two-dimensional dynamical system, which reads, in dimensionless form, ds dT = n - ns - si, (7.6) di dT - (n+ 8)itsi, where n = v / a = M/a. As before, it is easy to check that trajectories starting in T remain in T (see exercises). The fixed points of (7.6) in the (s, i) plane areP1 = (1,0) and P2 || A + P" a A ._i | a | 5': V V The Jacobian of (E) is Jls'i) : (nii s (7+0) and JlP1)=(0n 1(nl+5))' Whether P2 is in T depends on the parameters 6 and 1]. More precisely, P2 6 'T 4:) 0 1, P1 is the only fixed point in 'T and since the eigenvalues of J(P1) are 1] and 1 (1] + 6), P1 is a stable node. All of the trajectories starting in T must converge to this xed point. which means that in the long run there are only susceptible individuals in the population. This is because those who have recovered from the disease eventually die and are replaced by new- borns, who are susceptible. This is illustrated in Figure 7.2, which shows the phase por- trait of (E), obtained with PPLANE, with 6 = 0.2 and 1] = 1. s =n-ns-si n = 1 i' = -(nto)i+si 6= 0.2 TTTTTTTTTTTTTTT TTTTTTTTTTTTTTTT .~ 0.5 0 0 0.5 S Figure 7.2. Phase plane of system (7.6), with 6 = 0.2 and n = 1, plotted with the software PPLANE. Only the dynamics inside T (not shaded) is relevant. If on the other hand n + 8