Question: Problem 4 Partial derivatives. Consider the function defined by f (t. x, y) = ch() sin(mx) cos(ny) where m and n are two arbitrary parameters.

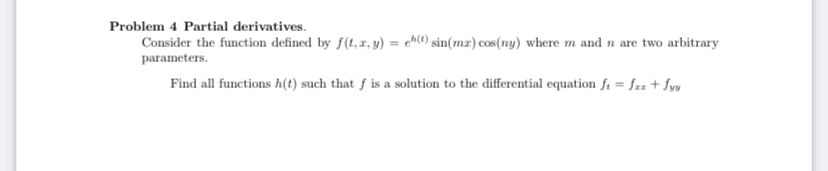
Problem 4 Partial derivatives. Consider the function defined by f (t. x, y) = ch() sin(mx) cos(ny) where m and n are two arbitrary parameters. Find all functions h(t) such that f is a solution to the differential equation fi = fix + fvyProblem 3 Limit and Continuity. (i) At what points is f(x, y) continuous? f(x,y) = 13 + 12: (x, y) # (0.0). 1: (r, y) = (0. 0). (ii) Find lim(z.v)-+(0,0) r+12 /x3+ 12+4 -2

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

seventh pages Chapter 3 Curve Sketching How much metal would be required to make a 400-mL soup can? What is the least amount of cardboard needed to build a box that holds 3000 cm3 of cereal? The...

ANSI-SPARC6 Programming Language Compilation Write notes on each of the following topics: (a) the implementation of labels and jumps in a recursive, block structured programming language [7 marks]...

UNIVERISTY HELPP IN HERE NOT for TUTOR: dont submit if you dont do full THEM OR BAD RATE And in full explanation show all your work Solve the following system of nonlinear equations:x^2 + y^2 = 9 x^2...

1) State the initial value theorem. Verify the theorem for the functions (a) 3 4 sin t (b) (t 4)2 and state their initial values. [(a) 3 (b) 16] 2. Verify the initial value theorem for the voltage...

MA 261 PRACTICE PROBLEMS 1. If the line ` has symmetric equations y x1 z+2 2 = 3 = 7 , nd a vector equation for the line `0 that contains the point (2; 1; 3) and is parallel to `. A. ~ = (1 + 2t)~...

MAI1290C24 Assignment Lesson 2_Homework due 05/22/2024 at 11:59pm EDT Problem 1. (1 point) The equation of the line that goes through (-9, 6) and (5,3) can be written in the form y = mx+ b, where m=...

Use MATLAB to solve the problem. Please fill in the following code to solve problem 1 (given below codes). Part I and part II should be saved in different files and part II depends on the function...

But the formulas we used in MTH220 only applied to functions of a single variable x. Is it possible to use finite differences to estimate the partial derivatives of a function of the two variables x...

1. [-/1 Points] DETAILS SCALCET9 14.4.001. The graph of a function f is shown below. Graph Graph Description Interactive 3D Graph Help Find an equation of the tangent plane to the surface z = f(x, y)...

11:56 PP - 1CO 0 & O all all 53% Edit 30 X STATE UNIVERSITY OF NEW YORK AT ALBANY Department of Economics Ph. D. Comprehensive Examination: Macroeconomics June, 2017 Section 1. (Suggested Time: 45...

9. Carrier signal in a double sideband - carrier band system, c (t) = Acos (2nfc t) and the message signal m(t) = sinc (t) +sinc (t) Find the frequency domain expression and bandwidth of the...

A dairy farmer is considering optimizing the production of his dairy cows while minimizing the cost of the animal feeds. From past records, his animals consume 11 units of carb and 5 units of...

Which of the following situations, involving eliminations as part of the consolidation process, would not have implications for the calculation of non - controlling interest? the sale of inventory by...

Perform competitive advantage analysis for Anandam and hightlight 3-5 differentiators Perform industry analysis and define innovation and invention parameters (you can use online resources including...

1. The purpose of this chapter is to describe the key principles, procedures and strategies of personal communication benchmarking, as understood in this context.

1. Set a personal goal for yourself in your work situation. Examine this goal in the light of the 10 factors to achieve goals.

4. Set up at least one work role that is important for you to master. Reflect on how you can use your time more efficiently, not necessarily spend more time, to perform better in this work role.