Question: Problem 4: Subsequences Given a sequence X if there exists a strictly increasing sequence ,12, ,%) of indices of X such that for all j

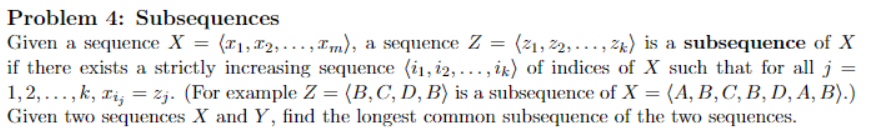
Problem 4: Subsequences Given a sequence X if there exists a

Problem 4: Subsequences Given a sequence X if there exists a strictly increasing sequence ,12, ,%) of indices of X such that for all j 1, 2, . . . , k, zy-Sj. (For example Z = B, C, D, B) is a subsequence of X = (A, B, C, B, D, A, B).) Given two sequences X and Y, find the longest common subsequence of the two sequences. = (zl ,T2, . . . ,z,n), a sequence Z =21:22, , zx) is a subsequence of X

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

java Bitonic Sequence is a sequence of numbers which is first strictly increasing then after a point strictly decreasing. The longest bitonic subarray problem is to find a subarray of a given...

CpE 207 Data Structures Fall 2021 use java language when write algorithm Q3 [10 pts] A Bitonic Sequence is a sequence of numbers which is first strictly increasing then after a point strictly...

Question 4 Longest increasing subsequence: Given an input sequence X = (21,22, ..., 2n) of numbers, an increasing subsequence of X is a subsequence where the values are increasing in value. We would...

ECE 502 Sep 6th Probability and Random Processes Homework Assignment 2 Fall 2016 due Sep 15th Problem 1: (25 points) Model homework problem 10 from assignment 1 in MATLAB and determine...

Page 236: Ex5B-8. Utilize the Outdoor Clubs & Product database to create a procedure "ex5b_supplier_update" that contains two input parameters. The first input parameter is a supplier_id attribute...

Describe five physical properties of a communications channel. [5 marks] (b) Consider the figure below. Entities N and N0 use an ARQ system. Channel - 1 Channel Channel + 1 Entity - 1 Entity Entity +...

Problem 5 (3 points each) In this problem, we will see another helpful way of interpreting the definition of the limit of a sequence. Definition. Given a sequence {x,} and a predicate P(r), we say...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

1. (60 pts True/False. Indicate whether the statement is true or false. If the statement is false, present an explanation or counterexample. (No explanation necessary for each true statement.) (2...

A rectangular solid made of carbon has sides of lengths 1.0 cm, 2.0 cm, and 4.0 cm, lying along the x, y, and z axes, respectively (Fig. 18-35). Determine the resistance for current that passes...

The Securities and Exchange Board of India received serious complaints against Mr. Satyanarayan, a member of the Mavli Stock Exchange. State as to what powers can be exercised by the Securities and...

The Index represents the performance of the Japanese stock market. Multiple Choice DAX FTSE Nikkel Hang Seng

ieconchilation? Choose the correct answer Wechontion? Choose thit corcectisher Noine of theabove ale deposits in transir on 12731/23 P.8-3b. Adjusting inventory Suggestan internal control that would...

4. Trainees and their managers provide estimates of training benefits.

2. Place a value on the outcomes.

4. Obtain an annual amount of benefits (operational results) from training by comparing results after training to results before training (in dollars).