Question: Problem 4. The nth Fibonacci number F is defined by Fo= 0, F = 1, and Fn+2 = Fn+1+F, 80 F = 1 F3

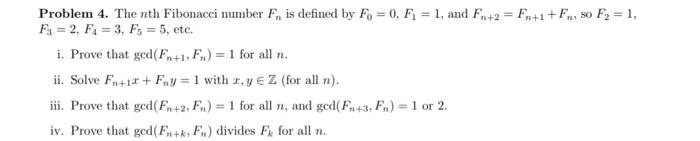
Problem 4. The nth Fibonacci number F is defined by Fo= 0,

Problem 4. The nth Fibonacci number F is defined by Fo= 0, F = 1, and Fn+2 = Fn+1+F, 80 F = 1 F3 = 2, F3, F5 = 5, etc. i. Prove that ged(Fn+1, Fn) = 1 for all n. ii. Solve Fn+12+ Fay =1 with r, y Z (for all n). iii. Prove that ged(Fn+2, Fn) = 1 for all n, and gcd(Fn+3+ Fn) = 1 or 2. iv. Prove that ged(Fn+k+ Fn) divides F for all n.

Step by Step Solution

★★★★★

3.36 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

solution iWe can prove this statement by induction on n Base Case n 0 F1 1 and F0 0 so gcdF1 F0 1 Inductive Step assume gcdFn1 Fn 1 for some n We must ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Feedback Check My Work Incorrect Schedule 3 Complete the Arc's Schedule 3. SCHEDULE 3 OMB No. 1545-0074 (Form 1040) Additional Credits and Payments 2023 Department of the Treasury Attach to Form...

The function f is defined by f(x) = (x - 1) 2 + 3 for x > - 1. The function g is defined by g(x) = 2x + 4/x - 5 for x > 5. Find fg(7).

The function f is defined by f: x 10 - (x - 3) 2 for 2 x 7. Find the range of f.

The function f is defined by f(x) = (2x + 1) 2 - 5 for x - 1/2. Find the range of f.

This problem compares the efficiency of three methods for computing the nth Fibonacci number F n , givenn. Assume that the cost of adding, subtracting, or multiplying two numbers isO(1), independent...

The Fibonacci sequence occurs frequently in nature as the growth rate for certain idealized animal populations. The sequence begins with 0 and 1, and each successive Fibonacci number is the sum of...

1. The nth Fibonacci binary tree F is defined recursively as follows. F is a single root node with no children. For all n 2, Fn is obtained from F-1 by adding a right child to every leaf and adding...

For n > 0 let Fn denote the nth Fibonacci number. Prove that Fo + Fi + F2 +. + F, =F = Fa42 - 1. 1=0

Mathematicians talk about the Fibonacci Sequence, which is a series of numbers defined recursively. The first Fibonacci number is 0, and the second is 1. From there on out, the nth Fibonacci number...

Show that the Maclaurin series for the function g(x) is 00 n=1 = X 1 - x - x Fx n where F is the nth Fibonacci number with F = F = 1 and F = Fn-2+ F-1, for n 3. Fn Write X ao + ax + ax + 1- x - x...

Calculate the first four terms of the sequence, starting with n = 1. an Fn+1 Fn where Fn is the nth Fibonacci number.

The free cash flow valuation model described in CH 7 is a very powerful model that can be used to value stocks businesses and divisions of businesses What are the most important drivers of value in...

estion 20 Assume that we have two events, A and B, that are independent ot yet swered events. Assume further that we know P(A) =0.50 and P(B) =0.40. Find P(A|B) arked out of Select one: Flag question...

DP9.3 An automatic drug delivery system is used in the regulation of critical care patients suffering from car diac failure [24]. The goal is to maintain stable patient status within narrow bounds....

Contrast the income statement effect of LIFO versus FIFO (i.e., on pretax income) when (a) Prices are rising and (b) Prices are falling.

Contrast the effects of LIFO versus FIFO on cash outflow and inflow.

Explain briefly the application of the LCM concept to the ending inventory and its effect on the income statement and balance sheet when market is lower than cost.

(a). Juan Marichal believes that the analysis of financial statements is directed at two characteristics of a company: Liquidity and profitability. Is Juan correct? Explain. (b). Are short-term...

The return on assets for Tresh Corporation is 7.6%. During the same year Treshs return on common stockholders equity is 12.8%.What is the explanation for the difference in the two rates?

7. . Calculate and interpret the odds ratio for the data in this table. Please show your work for the calculation. COVID-19 Positive COVID-19 Negative YesConsistent Mask Use 53,947 488,419 NoNot...

n- Let fn be the nth Fibonacci number, i.e. we will let fo = 0, f = 1, and then fn = fn1 + n2 for all n 2 (so f = 1, f3 = 2, f4 = 5, f5 = 8, f6 = 13, and so forth). Prove using induction that f2 n 1...

This is a C++ problem. Please give full explanation and code in details. Thanks. Fibonacci numbers arise in a number of different places and are related to the golden ratio. Fibonacci numbers are...

CAN SOMEONE PLEASE HELP ME AND GIVE EXPLANATION? THANKS! THUMBS UP WILL BE GIVEN 2. The n-th Fibonacci num ber F, is defined recursively as Fn = Fn-1 + Fn-2, where Fo = 0 and Fi = 1. A naive...

1. Your favorite local coffee shop currently employs 10 people, and produces 100 cups of coffee per day. In an effort to expand, they hire 10 more people, and can now produce 175 cups of coffee per...

Solving this task with recursion in c++: PLZ write every class with their own file, you should include the flowing files: Reverse.cpp Reverse.h Fibonacci.cpp Fibonacci.h EfficientFibonacci.cpp...

Rewrite the following nested if-else statement as a switch statement that accomplishes exactly the same thing. Assume that num is an integer variable that has been initialized, and that there are...