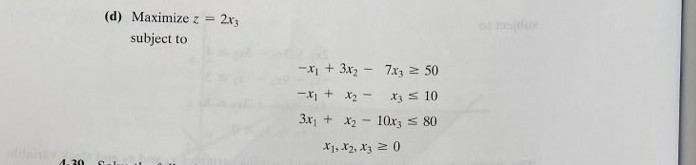
problem. 4-38. Using the artificial constraint procedure introduced in Problem 4-37, solve the following problems by the dual simplex method. In each case, indicate whether the resulting solu- tion is feasible, infeasible, or unbounded. The starting basic solution consisting of surplus variables x4 and xs and slack variable Xo is infeasible because x = -4 and xs = -3. However, the dual simplex is not appli- cable directly, because X1 and xz do not satisfy the maximization optimality condition. Show that by adding the artificial constraint x1 + x3 = M (where M is sufficiently large not to eliminate any feasible points in the original solution space), and then using the new constraint as a pivot row, the selection of x as the entering variable (because it has the most negative objective coefficient) will render an all-optimal objective row. Next, carry out the regular dual simplex method on the modified problem. (d) Maximize z = subject to 2x3 X'; 10 -X1 + 3x2 - 7x3 50 -x + x2 3.x1 + x2 - 10x3 = 80 X1, X2, X3 20 30 problem. 4-38. Using the artificial constraint procedure introduced in Problem 4-37, solve the following problems by the dual simplex method. In each case, indicate whether the resulting solu- tion is feasible, infeasible, or unbounded. The starting basic solution consisting of surplus variables x4 and xs and slack variable Xo is infeasible because x = -4 and xs = -3. However, the dual simplex is not appli- cable directly, because X1 and xz do not satisfy the maximization optimality condition. Show that by adding the artificial constraint x1 + x3 = M (where M is sufficiently large not to eliminate any feasible points in the original solution space), and then using the new constraint as a pivot row, the selection of x as the entering variable (because it has the most negative objective coefficient) will render an all-optimal objective row. Next, carry out the regular dual simplex method on the modified problem. (d) Maximize z = subject to 2x3 X'; 10 -X1 + 3x2 - 7x3 50 -x + x2 3.x1 + x2 - 10x3 = 80 X1, X2, X3 20 30