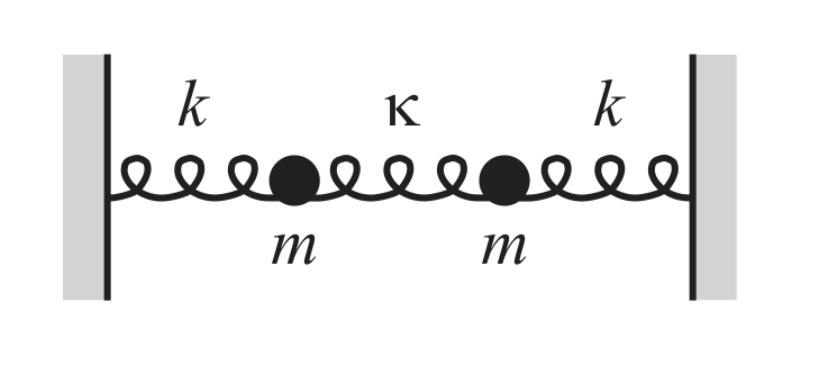
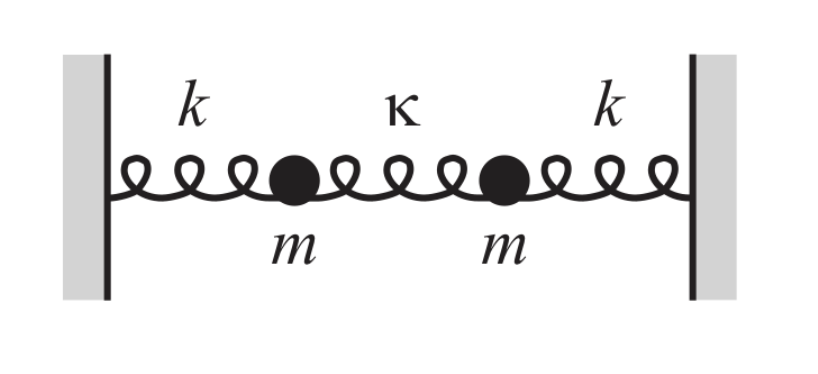
Problem 5 (40 points): Three springs and two equal masses (m) are connected /attached between two walls, as shown in the figure below. The spring constant of the lateral springs is k, while the one at the middle is k. (a) Find the general solution for both positions of the masses and discuss what are the normal modes of this system (20 points). (b) First assume that k > , then let z; () and z2 () be the positions of the left and right masses, respectively, relative to their equilibrium positions. If the initial positions are given by z; (t = 0) = xy and x5 (t) = 0, and if both masses are released from rest, show that z; (t) and x5 (t) can be written as x1 (t)=z( cos [(wy + ) t] cos [et] (7) Zs (t)=xq sin [(wg + ) t] sin [et] (8) with wo = v/k/m and = $-wo. (20 points) k K k m m