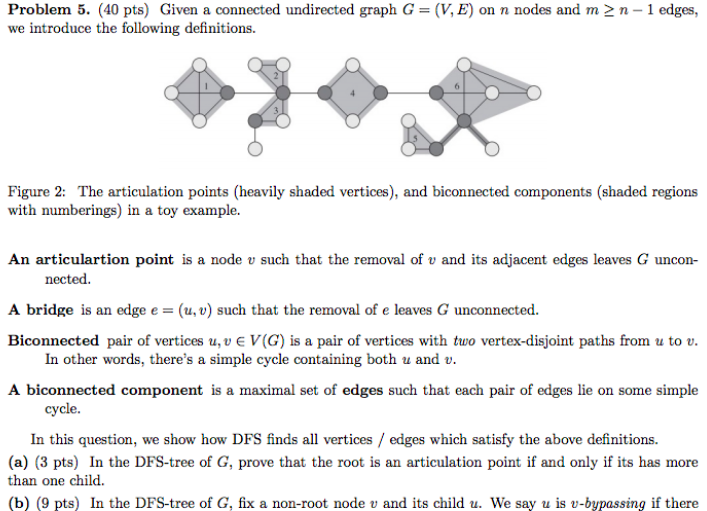
Problem 5. (40 pts) Given a connected undirected graph G = (V, E) on n nodes and m 2 n-1 edges, we introduce the following definitions. Figure 2: The articulation points (heavily shaded vertices), and biconnected components (shaded regions with numberings) in a toy example. An articulartion point is a node v such that the removal of v and its adjacent edges leaves G uncon- A bridge is an edge e = (u,v) such that the removal of e leaves G unconnected. Biconnected pair of vertices u,u E V(G) is a pair of vertices with two vertex-disjoint paths from u to v. A biconnected component is a maximal set of edges such that each pair of edges lie on some simple nected. In other words, there's a simple cycle containing both u and v cycle In this question, we show how DFS finds all vertices/ edges which satisfy the above definitions. (a) (3 pts) In the DFS-tree of G, prove that the root is an articulation point if and only if its has more than one child b) (9 pts) In the DFS-tree of G, fix a non-root node v and its child u. We say u is v-bypassing if there