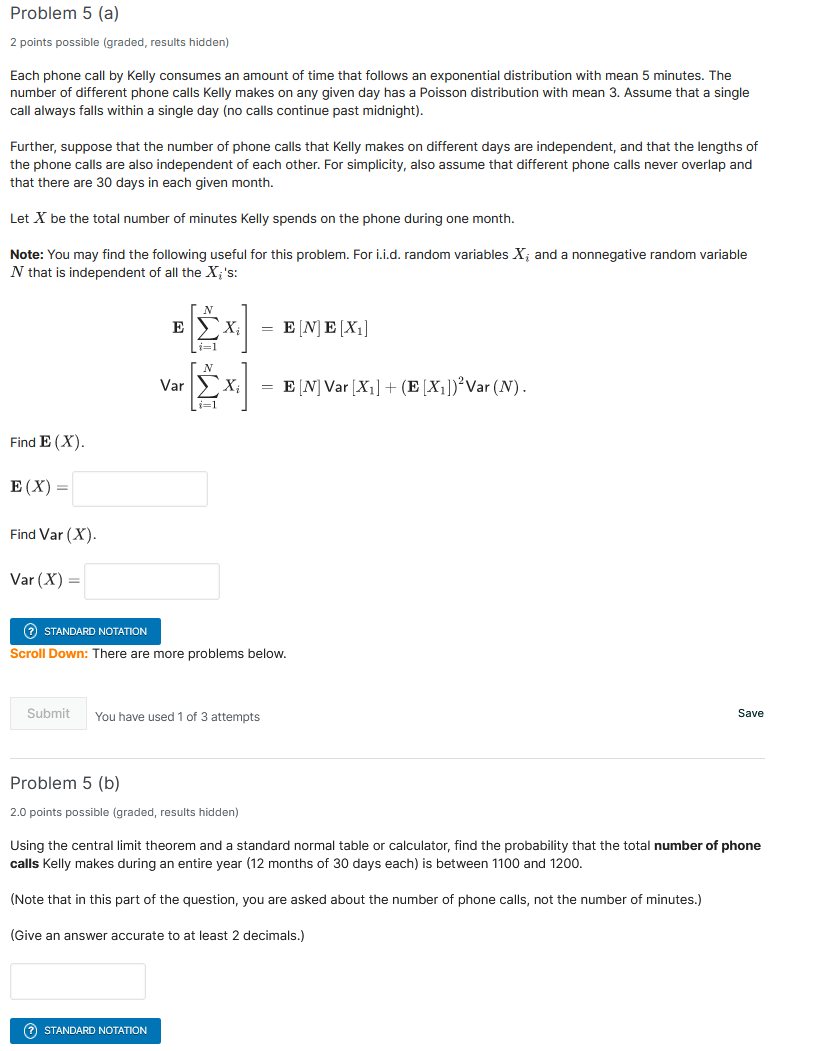
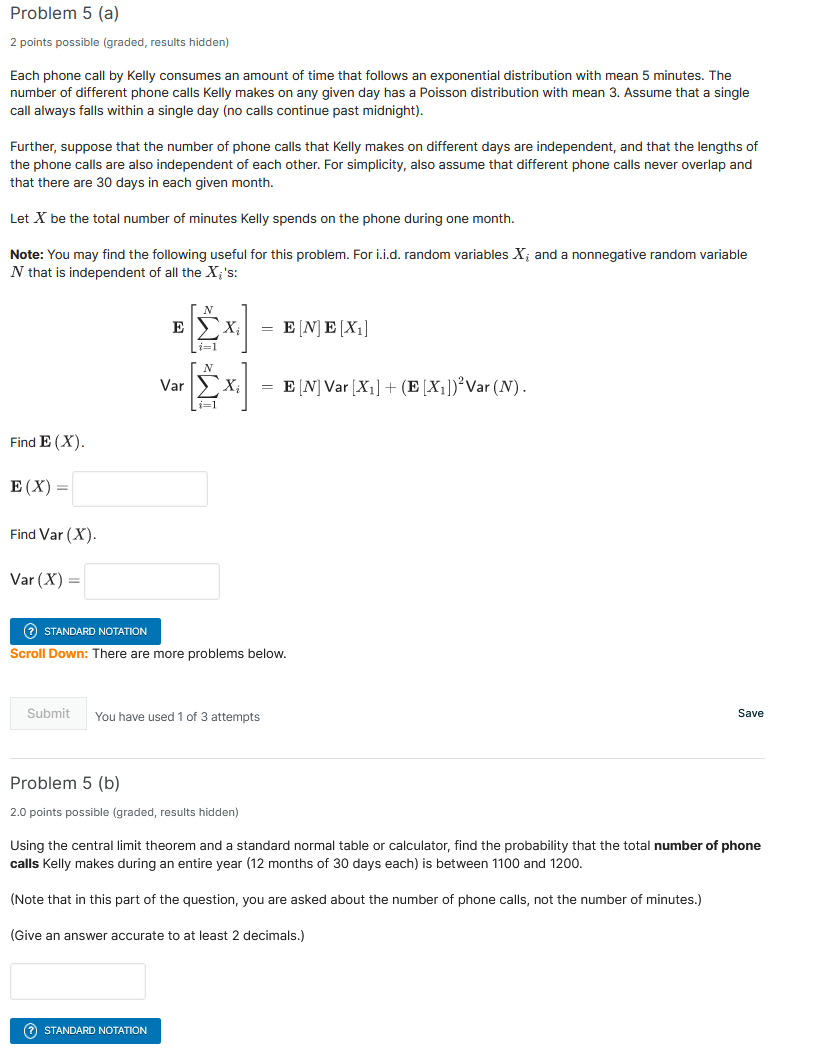
Problem 5 (a) 2 points possible (graded, results hidden) Each phone call by Kelly consumes an amount of time that follows an exponential distribution with mean 5 minutes. The number of different phone calls Kelly makes on any given day has a Poisson distribution with mean 3. Assume that a single call always falls within a single day (no calls continue past midnight). Further, suppose that the number of phone calls that Kelly makes on different days are independent, and that the lengths of the phone calls are also independent of each other. For simplicity, also assume that different phone calls never overlap and that there are 30 days in each given month. Let X be the total number of minutes Kelly spends on the phone during one month. Note: You may find the following useful for this problem. For i.i.d. random variables X, and a nonnegative random variable N that is independent of all the X;'s: E Xi = EMEXI ] 1=1 Var CXi = E [N] Var [Xi] + (E [Xi])' Var (N) . Find E (X) E(X) = Find Var (X). Var (X) = 2 STANDARD NOTATION Scroll Down: There are more problems below. Submit You have used 1 of 3 attempts Save Problem 5 (b) 2.0 points possible (graded, results hidden) Using the central limit theorem and a standard normal table or calculator, find the probability that the total number of phone calls Kelly makes during an entire year (12 months of 30 days each) is between 1100 and 1200. (Note that in this part of the question, you are asked about the number of phone calls, not the number of minutes.) (Give an answer accurate to at least 2 decimals.) (?) STANDARD NOTATION