PROBLEM 5

(a) Consider the shaded region D0 from Problem 4 above, and assume it represents a lamina with density function ?(x, y) = y. Use Green's theorem to find in an alternate way its total mass.

(b) Consider the shaded region D1 from page 6 of this file, which is the region enclosed by the circle x^2 + (y-3)^2 = 16 and found outside the ellipse x^2 + 2y^2 = 1.

Compute its area, as well as its centroid (that is, the centre of mass when the density is uniform and equal to 1 everywhere) using Green's theorem.

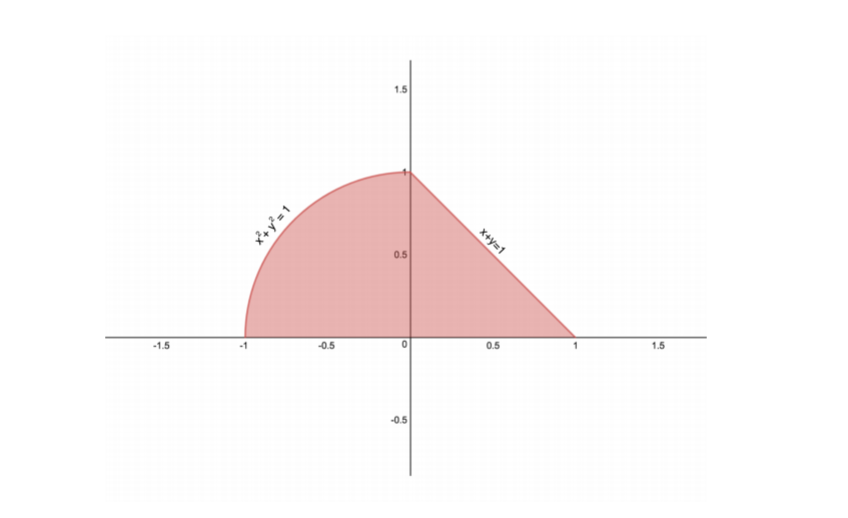
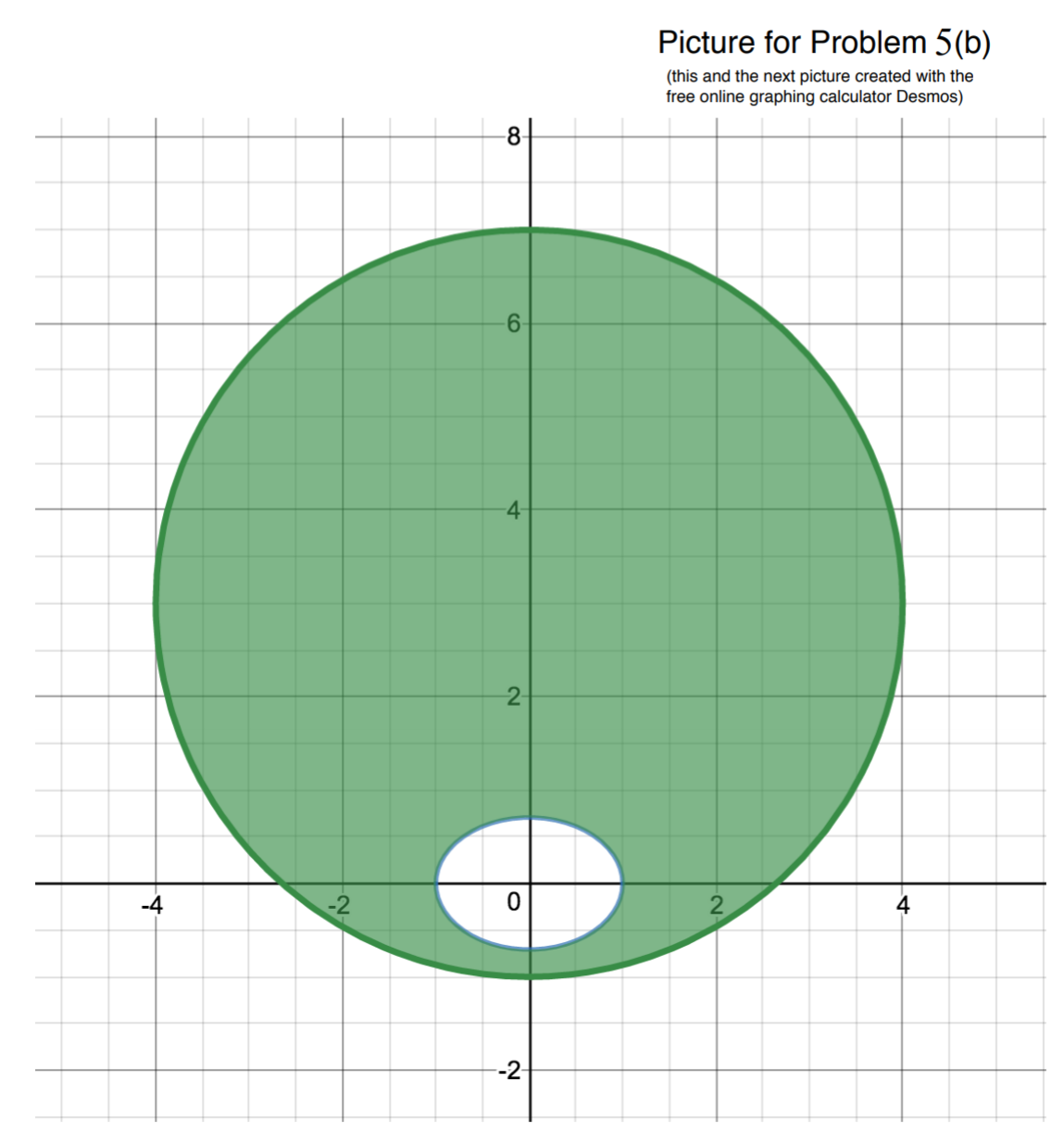
[Hint for part (a). First of all, note that in Problem 4 you are already asked to nd a parametrisation of the boundary of the region Do. Is the orientation given by the parametrisation(s) you will have found suitable for this problem too, or do you need to adjust the parametrisation? Secondly, you are told that the mass density over this region is given by the function p(a:, y): therefore moo = If ydA. In order to be able to apply Green' s theorem and equate this double integral with a line integral of a vector eld along the boundary of Do, you need to nd a continuously differentiable vector eld F: Pi + Q 3 such that 362 3? 63 _ 61; 3" (why?). There is no canonical choice here, and you can nd several such vector elds, but some choices are easier to come up with than others. For example, we could rst choose to set one of the component functions of F equal to 0: if we set P = 0, we could then go on to choose Q(x y) my, and thus F{x,y) = (0,321; if we set Q = 0, then we could go on to choose P(a:,y)= 3, and thus F (m y): { 192/2, 0). Moreover, another choice that could work here is F012, 3;) = (y2, 3;y) (check it). Just for practice, try to come up with a few more choice; of vector elds F (m, y) that would allow you to solve part (a). What is another criterion we could have for considering some of these choices better than others?] \fPicture for Problem 5(b) (this and the next picture created with the free online graphing calculator Desmns)