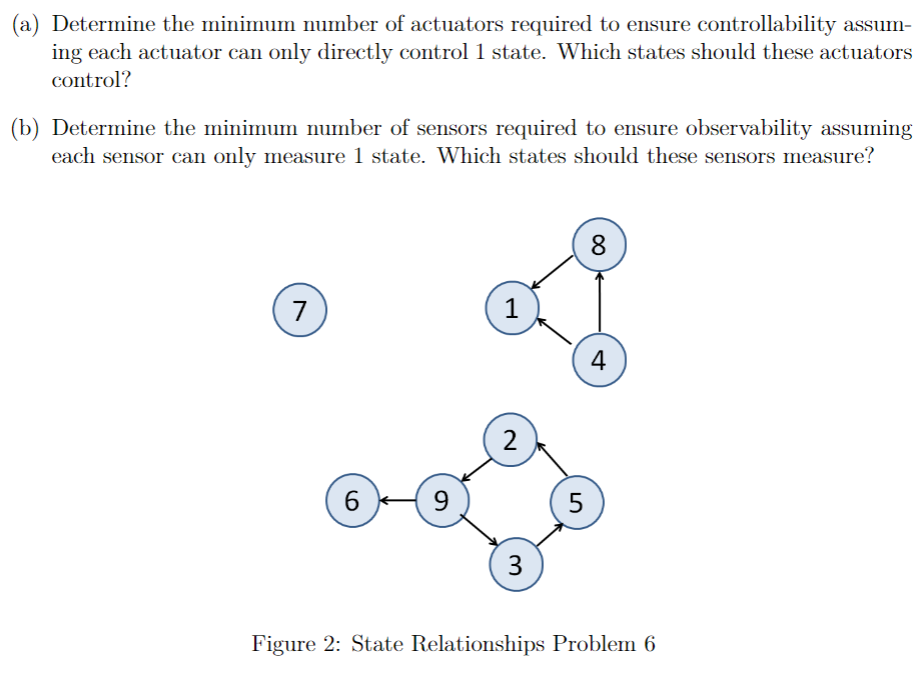
Question: Problem 5. Sensor and Actuator Placement (12 points) In the figure below, each node represents a state of a LTI dynamical system whose dynamics are

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


