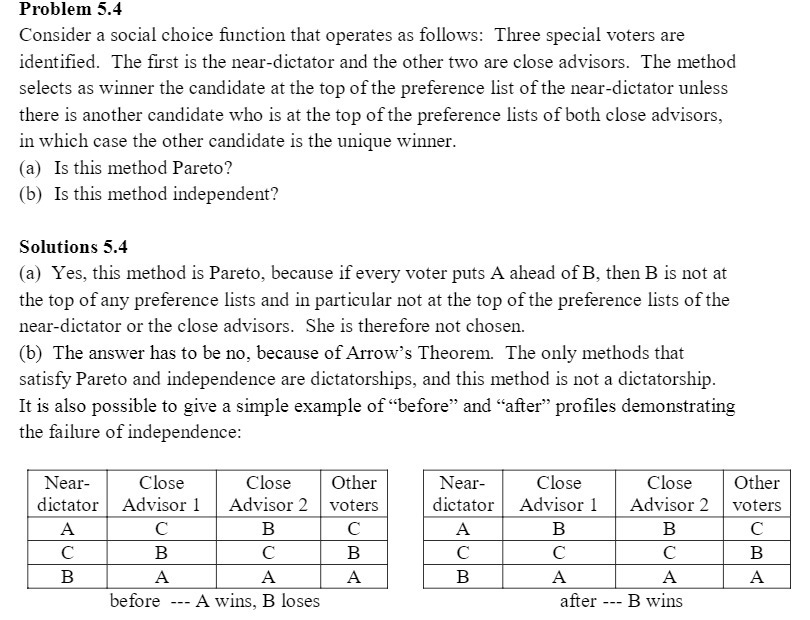
Question: Problem 5.4 Consider a social choice mction that operates as follows: Three special voters are identied. The rst is the near-dictator and the other two
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


