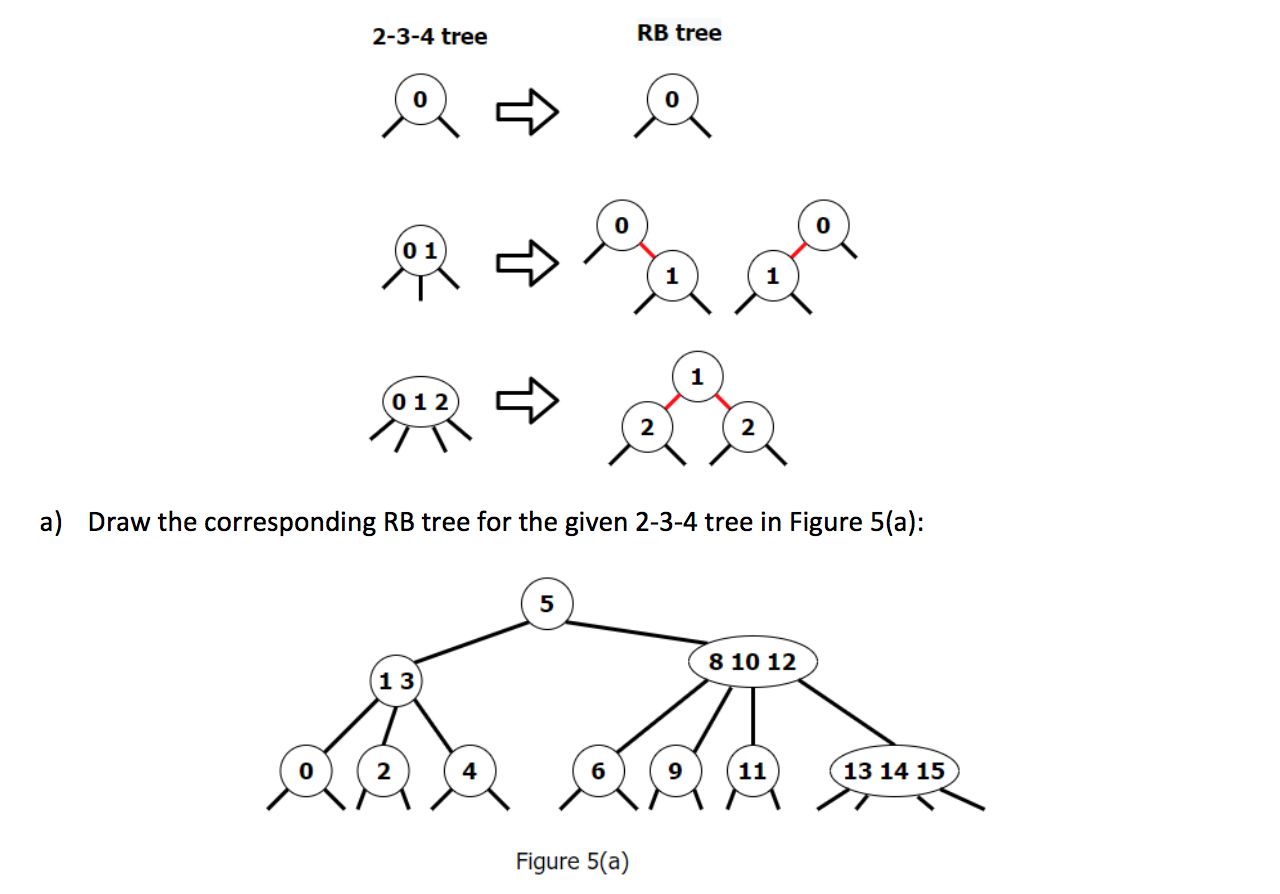
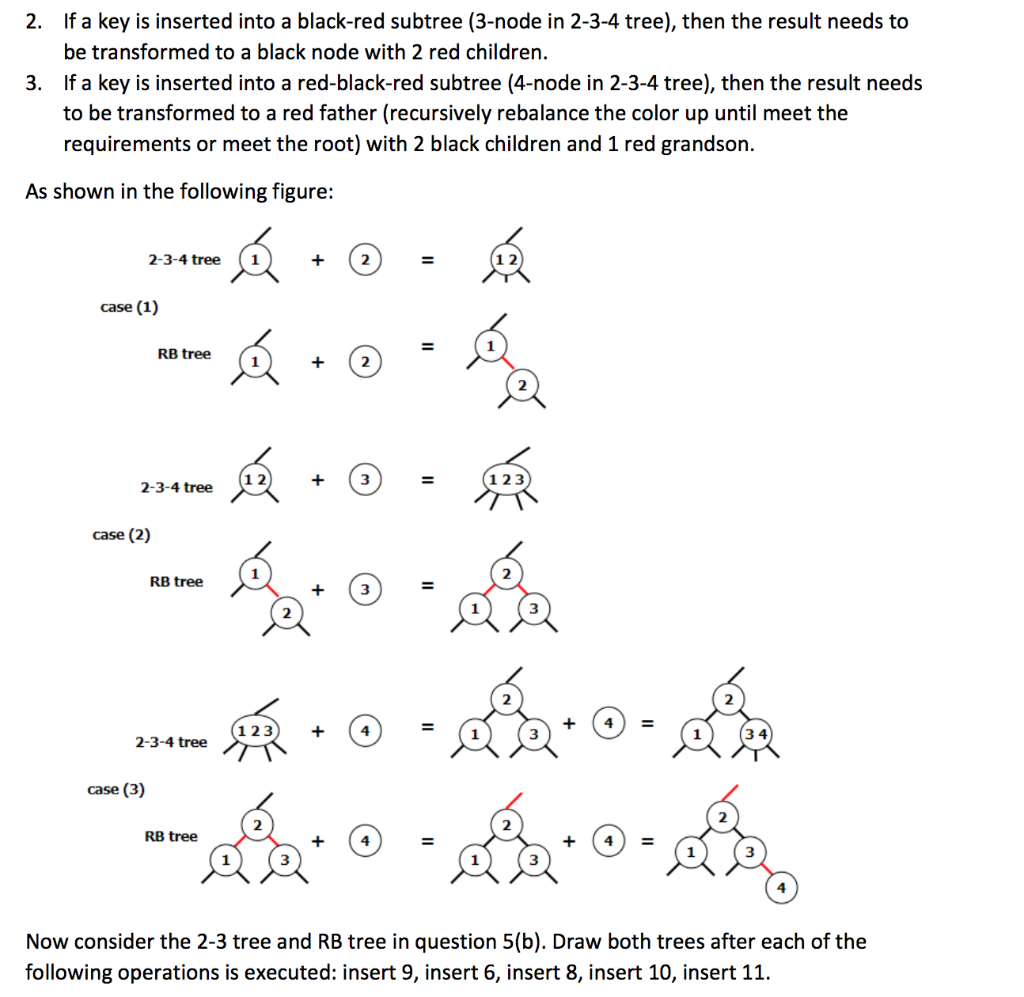
Problem 6 (20 points): The LLRB tree is a variant of RB tree, which is a lot easier to implement in code. Considering the general RB tree, which does not require red nodes to be linked to the left. That is, a node could have a left red child, or a right red child, or even two red children. But a red node must have black children. Like that LLRB tree represents 2-3 tree, the general RB tree represents 2-3-4 tree, where a node is allowed to have 1 key and 2 links (2-node), or 2 keys and 3 links (3-nodes), or 3 keys and 4 links (4-nodes). The relationship between RB tree and 2-3-4 tree is that: A 2-node in 2-3-4 tree is a black node with no red child in RB tree. A 3-node in 2-3-4 tree is a black node with 1 red child in RB tree. A 4-node in 2-3-4 tree is a black node with 2 red children in RB tree. As shown in the following figure: 2-3-4 tree RB tree (0) ) 0 1 012 2 a) Draw the corresponding RB tree for the given 2-3-4 tree in Figure 5(a): 5 8 10 12 13 4 11 13 14 15 Figure 5(a) b) Draw the corresponding 2-3-4 tree for the given RB tree: 3 0 2 4 Figure 5(b) c) Considering the insert operation in 2-3-4 tree and RB tree: 1. If a key is inserted into a 2-node, the 2-node becomes a 3-node. 2. If a key is inserted into a 3-node, the 3-node becomes a 4-node. 3. If a key is inserted into a 4-node, firstly, the middle value in the 4-node is added to the father node (if the father is also a 4-node, recursively split the father and add the middle value to the grandfather; if the father is a 4-node root, then split it and make the middle value a new root, and the tree height plus 1), and the left and right values becomes two 2- nodes children. Then, new key is inserted into the corresponding child and makes it to a 3- node. The corresponding rules of insert operation in RB tree are: 1. If a key is inserted into a black node with no red child (2-node in 2-3-4 tree), then insert it as a red child to that node. 2. If a key is inserted into a black-red subtree (3-node in 2-3-4 tree), then the result needs to be transformed to a black node with 2 red children. 3. If a key is inserted into a red-black-red subtree (4-node in 2-3-4 tree), then the result needs to be transformed to a red father (recursively rebalance the color up until meet the requirements or meet the root) with 2 black children and 1 red grandson. As shown in the following figure: 2-3-4 tree 1 + 2 = case (1) RB tree en 3 = 2-3-4 tree case (2) RB tree ce 2-3-4 tree case (3) RB tree A. O - - - - Now consider the 2-3 tree and RB tree in question 5(b). Draw both trees after each of the following operations is executed: insert 9, insert 6, insert 8, insert 10, insert 11. Problem 6 (20 points): The LLRB tree is a variant of RB tree, which is a lot easier to implement in code. Considering the general RB tree, which does not require red nodes to be linked to the left. That is, a node could have a left red child, or a right red child, or even two red children. But a red node must have black children. Like that LLRB tree represents 2-3 tree, the general RB tree represents 2-3-4 tree, where a node is allowed to have 1 key and 2 links (2-node), or 2 keys and 3 links (3-nodes), or 3 keys and 4 links (4-nodes). The relationship between RB tree and 2-3-4 tree is that: A 2-node in 2-3-4 tree is a black node with no red child in RB tree. A 3-node in 2-3-4 tree is a black node with 1 red child in RB tree. A 4-node in 2-3-4 tree is a black node with 2 red children in RB tree. As shown in the following figure: 2-3-4 tree RB tree (0) ) 0 1 012 2 a) Draw the corresponding RB tree for the given 2-3-4 tree in Figure 5(a): 5 8 10 12 13 4 11 13 14 15 Figure 5(a) b) Draw the corresponding 2-3-4 tree for the given RB tree: 3 0 2 4 Figure 5(b) c) Considering the insert operation in 2-3-4 tree and RB tree: 1. If a key is inserted into a 2-node, the 2-node becomes a 3-node. 2. If a key is inserted into a 3-node, the 3-node becomes a 4-node. 3. If a key is inserted into a 4-node, firstly, the middle value in the 4-node is added to the father node (if the father is also a 4-node, recursively split the father and add the middle value to the grandfather; if the father is a 4-node root, then split it and make the middle value a new root, and the tree height plus 1), and the left and right values becomes two 2- nodes children. Then, new key is inserted into the corresponding child and makes it to a 3- node. The corresponding rules of insert operation in RB tree are: 1. If a key is inserted into a black node with no red child (2-node in 2-3-4 tree), then insert it as a red child to that node. 2. If a key is inserted into a black-red subtree (3-node in 2-3-4 tree), then the result needs to be transformed to a black node with 2 red children. 3. If a key is inserted into a red-black-red subtree (4-node in 2-3-4 tree), then the result needs to be transformed to a red father (recursively rebalance the color up until meet the requirements or meet the root) with 2 black children and 1 red grandson. As shown in the following figure: 2-3-4 tree 1 + 2 = case (1) RB tree en 3 = 2-3-4 tree case (2) RB tree ce 2-3-4 tree case (3) RB tree A. O - - - - Now consider the 2-3 tree and RB tree in question 5(b). Draw both trees after each of the following operations is executed: insert 9, insert 6, insert 8, insert 10, insert 11