Question: Problem #6: Let f(x) = 1 + 8x - On what interval is f increasing? (A) (- In 7, ) (B) (-20, = In 8)
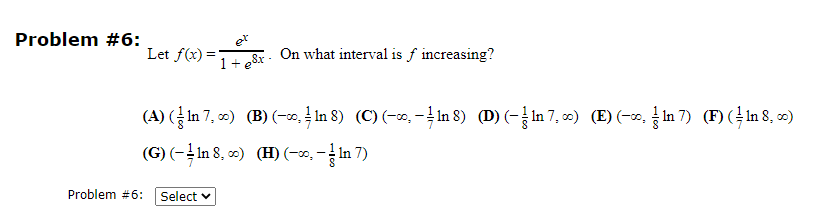


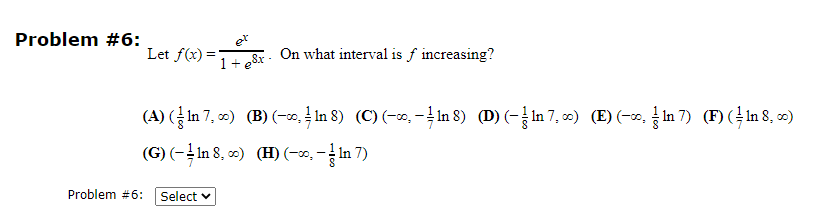
![Two critical values of the function x] = x35 (6 4x]. Enter](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66634f4a88639_39466634f4a77d46.jpg)

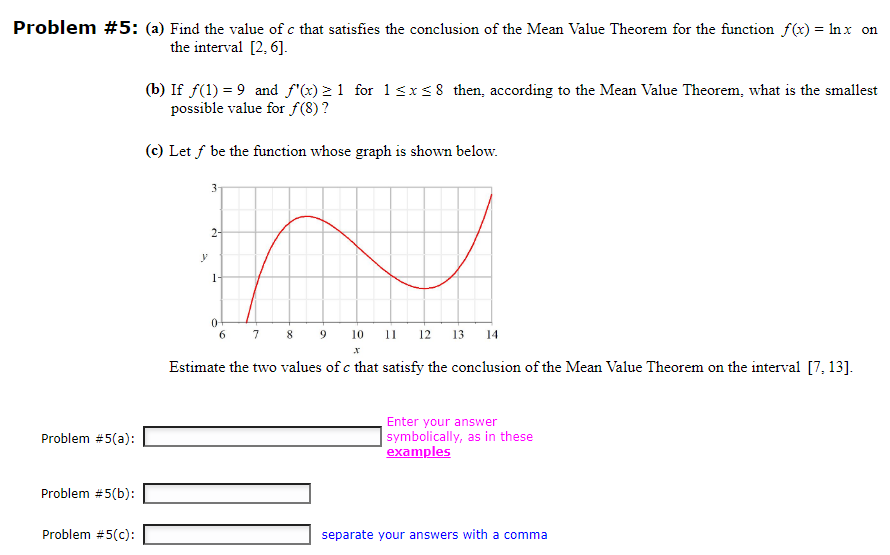
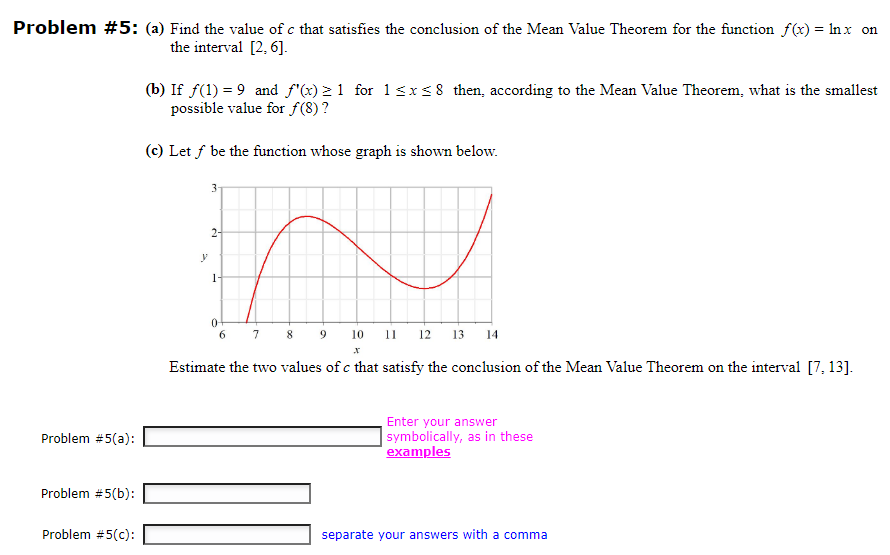
Problem #6: Let f(x) = 1 + 8x - On what interval is f increasing? (A) (- In 7, ) (B) (-20, = In 8) (C) (-, -1 8) (D) (- In7. ) (E) (-x, { In7) (F) (In8, .) (G) (- - In 8, 0) (H) (-, - - In 7) Problem #6: Select vProblem #3: Find the Two critical values of the function x] = x35 (6 4x]. Enter vow answer comma examples Problem #7: Let f(x) =x Inx. On what interval is f concave down? (A) ( e-11/30 60) (B) (0, 30/11 ) (C) ( e-30/11, co) (D) (30/11, co) (E) (ell /30 0) (F) (0, 0) (G) (0, e-11/30 ) (H) (0, el1/30 ) Problem #7: Select v Just Save Submit Problem #7 for Grading Problem #7 Attempt #1 Attempt #2 Attempt #3 Your Answer: Your Mark:Problem #5: (a) Find the value of c that satisfies the conclusion of the Mean Value Theorem for the function f(x) = Inx on the interval [2, 6]- (b) If f(1) = 9 and f'(x) 21 for 1x 8 then, according to the Mean Value Theorem, what is the smallest possible value for f(8) ? (c) Let f be the function whose graph is shown below. 2 0- 7 8 9 10 11 12 13 14 Estimate the two values of c that satisfy the conclusion of the Mean Value Theorem on the interval [7, 13]. Enter your answer Problem #5(a): symbolically, as in these examples Problem #5(b): Problem #5(c): separate your answers with a comma
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


