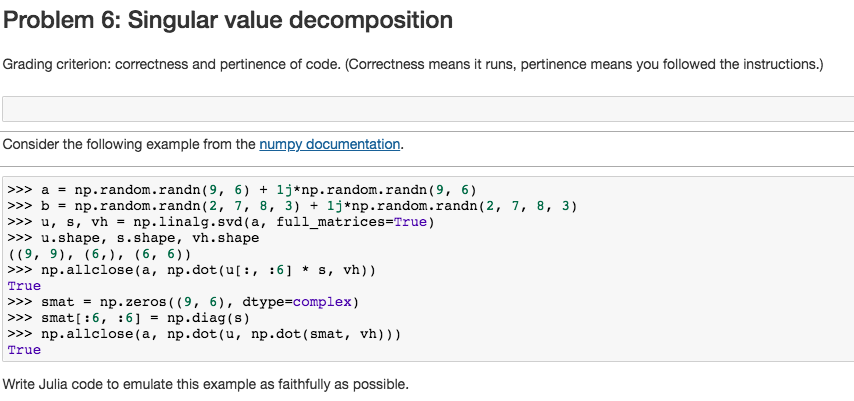
Problem 6: Singular value decomposition Grading criterion: correctness and pertinence of code. (Correctness means it runs, pertinence means you followed the instructions.) Consider the following example from the numpy documentation. >>> a np . random . randn ( 9, 6) + 1j*np.randon. randn ( 9, 6) >>> b= np.random . randn (2, 7, 8, 3) + 1j*np.random . randn(2, >>> u, s, vh = np.linalg.svd ( a, full-matrices*True) andom.randm(2, an-andn(2, 7, , 7, 8, 3) 3) u.shape, s.shape, vh.shape np.allclose(a, np.dot(ul:, :6]s, vh)) smat True >>> np . zeros ((9, 6), dtype-complex) aieoea, np.dot(u,' ap.dot( amat, vh) np.allclose(a, np.dot(u, np.dot (smat, vh))) True Write Julia code to emulate this example as faithfully as possible. Problem 6: Singular value decomposition Grading criterion: correctness and pertinence of code. (Correctness means it runs, pertinence means you followed the instructions.) Consider the following example from the numpy documentation. >>> a np . random . randn ( 9, 6) + 1j*np.randon. randn ( 9, 6) >>> b= np.random . randn (2, 7, 8, 3) + 1j*np.random . randn(2, >>> u, s, vh = np.linalg.svd ( a, full-matrices*True) andom.randm(2, an-andn(2, 7, , 7, 8, 3) 3) u.shape, s.shape, vh.shape np.allclose(a, np.dot(ul:, :6]s, vh)) smat True >>> np . zeros ((9, 6), dtype-complex) aieoea, np.dot(u,' ap.dot( amat, vh) np.allclose(a, np.dot(u, np.dot (smat, vh))) True Write Julia code to emulate this example as faithfully as possible