Problem 6-09 (Algorithmic) The Ace Manufacturing Company has orders for three similar products:

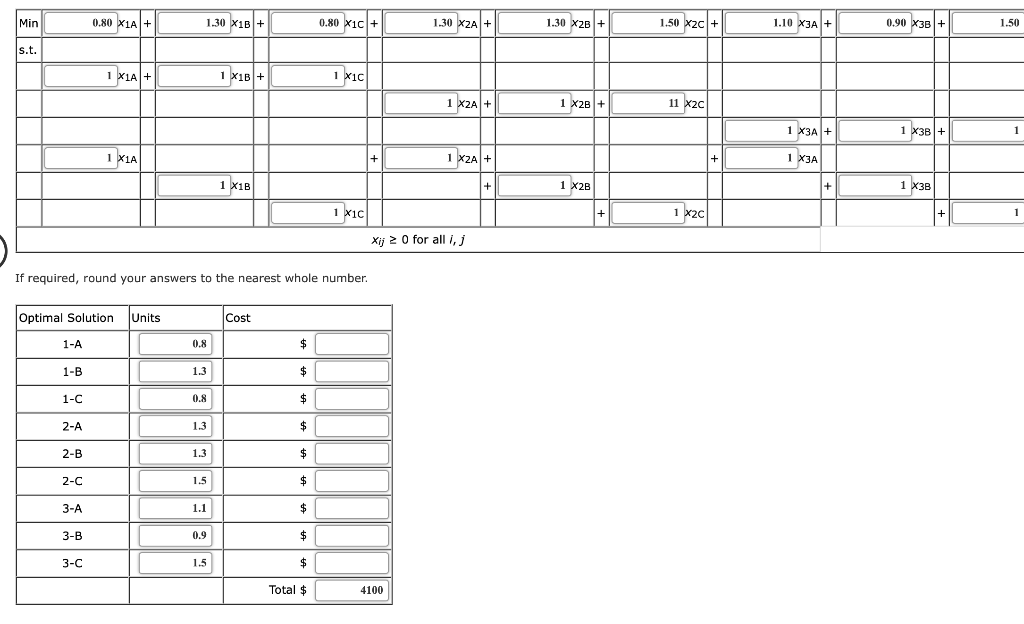
Problem 6-09 (Algorithmic) The Ace Manufacturing Company has orders for three similar products: Product Order (Units) 2050 500 1150 C Three machines are available for the manufacturing operations. All three machines can produce all the products at the same production rate. However, due to varying defect percentages of each product on each machine, the unit costs of the products vary depending on the machine used. Machine capacities for the next week and the unit costs are as follows: Machine Capacity (Units) 1500 1600 1000 WN Machine A $0.80 $1.30 $1.10 Product B $1.30 $1.30 $0.90 C $0.80 $1.50 2 3 $1.50 Use the transportation model to develop the minimum cost production schedule for the products and machines. Show the linear programming formulation. The linear programming formulation and optimal solution are shown. Let Xij = Units of product jon machine i. 0.80 X1A + 1.30 X1B + 0.80 x10 + 1.30 X2A + 1.50 xac + 1.10 X3A + 0.90 X38 + 1.50 1 X1A|+| 1 X1B + 1 xic 1 X2 + 1 X2B + 11 X2C 1 X3A + 1 xiA XZA + 1 X3 1X1C Xij 2 0 for all i, j If required, round your answers to the nearest whole number Optimal Solution Units Cost 1-A 1-B 1.3 0.8 1-C 2-B 1.3 1.5 2-C 3-A 3-B 3-C 1.5 Total $ 4100 Problem 6-09 (Algorithmic) The Ace Manufacturing Company has orders for three similar products: Product Order (Units) 2050 500 1150 C Three machines are available for the manufacturing operations. All three machines can produce all the products at the same production rate. However, due to varying defect percentages of each product on each machine, the unit costs of the products vary depending on the machine used. Machine capacities for the next week and the unit costs are as follows: Machine Capacity (Units) 1500 1600 1000 WN Machine A $0.80 $1.30 $1.10 Product B $1.30 $1.30 $0.90 C $0.80 $1.50 2 3 $1.50 Use the transportation model to develop the minimum cost production schedule for the products and machines. Show the linear programming formulation. The linear programming formulation and optimal solution are shown. Let Xij = Units of product jon machine i. 0.80 X1A + 1.30 X1B + 0.80 x10 + 1.30 X2A + 1.50 xac + 1.10 X3A + 0.90 X38 + 1.50 1 X1A|+| 1 X1B + 1 xic 1 X2 + 1 X2B + 11 X2C 1 X3A + 1 xiA XZA + 1 X3 1X1C Xij 2 0 for all i, j If required, round your answers to the nearest whole number Optimal Solution Units Cost 1-A 1-B 1.3 0.8 1-C 2-B 1.3 1.5 2-C 3-A 3-B 3-C 1.5 Total $ 4100