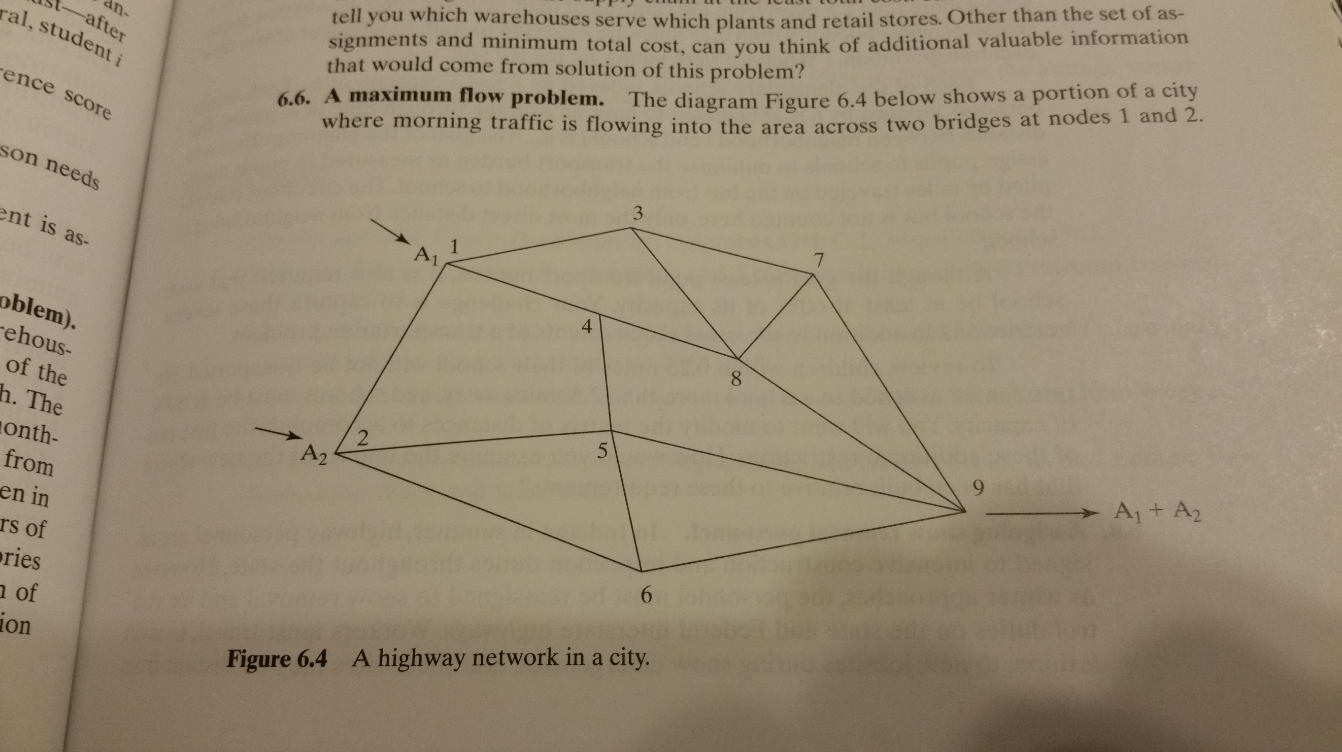
- Problem 6.6 from Revelle et al. You will formulate this problem mathematically, but you will not solve the problem. A maximum flow problem. The diagram below (Figure 6.4) shows a portion of a city where morning traffic is flowing into the area across two bridges at nodes 1 and 2 . Virtually all the traffic exits at node 9 to a manufacturing plant. On the link between any pair of noes i and j (intersections) is the capacity cij. This is the maximum flow in cars per hour on that link in the direction from i to j. An unknown amount of flow A1 enters at node 1 an an unknowns amount of flow A2 enters at node 2. The sum of the flows A1+A2 exits to the factory at node 9. The flows are unknowns because we are seeking the maximum flow through the system and motorists will divide themselves by experimentation into cars entering node 1 and cars entering node 2 . In general, motorists will not backtrack to gain advantage. In the evening, flows reverse and leave the factor to cross the area and exit via one of the two bridges. The flow capacities on each link are different now because the traffic is generally facing downhill into the setting sun. Set up a math program or programs that will find the maximum flow through the system. tell you which warehouses serve which plants and retail stores. Other than the set of assignments and minimum total cost, can you think of additional valuable information that would come from solution of this problem? 6.6. A maximum flow problem. The diagram Figure 6.4 below shows a portion of a city where morning traffic is flowing into the area across two bridges at nodes 1 and 2 . Figure 6.4 A highway network in a city