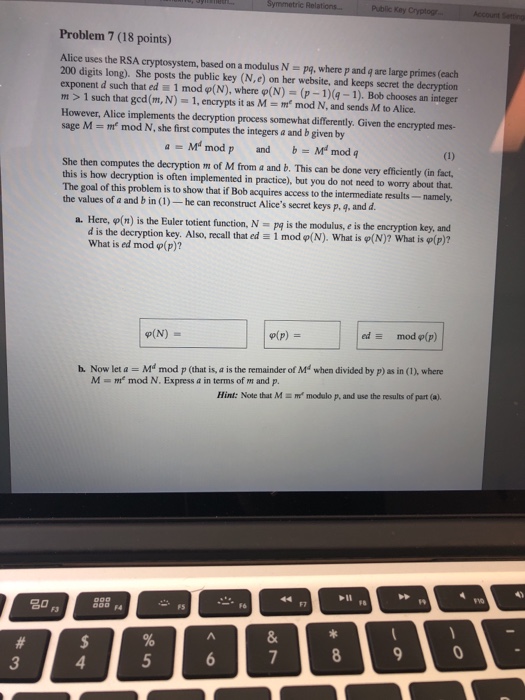
Problem 7 (18 points) Alice uses the RSA cryptosystem, based on a modulus N- pq, where p and q are large primes (each 200 digits long). She posts the public key (N,e) on her website, and keeps secret the decryption exponent d such that ed 1 mod p(N), where (N)-(p-1 )(q-1). Bob chooses an integer m >1 such that ged (m, N)-1, encrypts it as M- m mod N, and sends M to Alice. However, Alice implements the decryption process somewhat differently. Given the encrypted mes- sage M m mod N, she first computes the integers a and b given by a M mod p and bmodq She then computes the decryption m of M from a and b. This can be done very efficiently (in fact, this is how decryption is often implemented in practice), but you do not need to worry about that The goal of this problem is to show that if Bob acquires access to the intermediate results- namely, the values of a and b in (1)-he can reconstruct Alice's secret keys p. q, and d. a. Here, p(n) is the Euler totient function, N pg is the modulus, e is the encryption key, and 1 mod p(N), what is p(N)? what is pip)? d is the decryption key. Also, recall that ed What is ed mod (p)? ed mod p(p) (N) h. Now let a M mod p (that is, a is the remainder of Md when divided by p) as in (1), where Hint: Note that M m modulo p, and use the results of part (a). M=me mod N. Express a in terms of m and p. F7 20 a FS 3