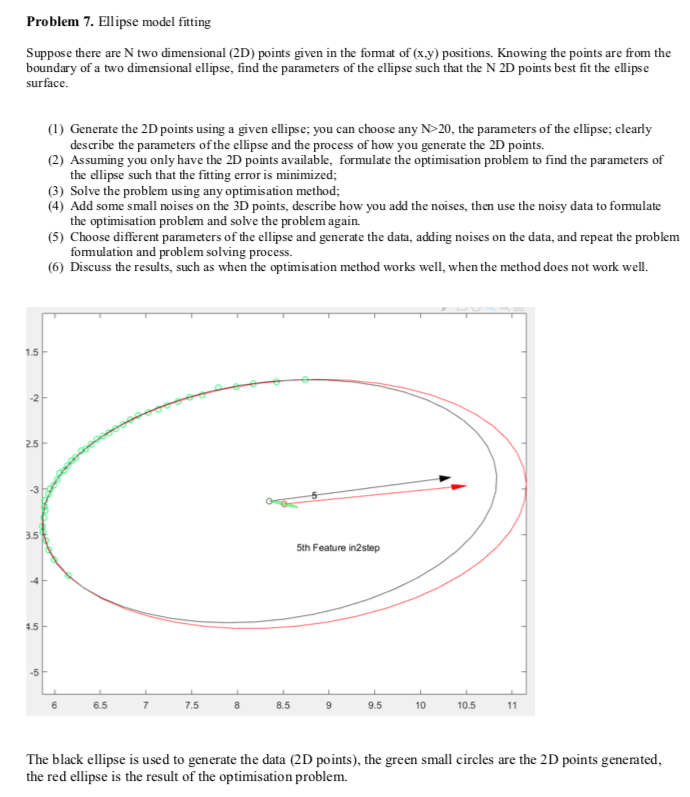
Problem 7. Ellipse model fitting Suppose there are N two dimensional (2D) points given in the format of (x,y) positions. Knowing the points are from the boundary of a two dimensional ellipse, find the parameters of the ellipse such that the N 2D points best fit the ellipse surface. (1) Generate the 2D points using a given ellipse; you can choose any N>20, the parameters of the ellipse; clearly describe the parameters of the ellipse and the process of how you generate the 2D points. (2) Assuming you only have the 2D points available, formulate the optimisation problem to find the parameters of the ellipse such that the fitting error is minimized; (3) Solve the problem using any optimisation method; (4) Add some small noises on the 3D points, describe how you add the noises, then use the noisy data to formulate the optimisation problem and solve the problem again. (5) Choose different parameters of the ellipse and generate the data, adding noises on the data, and repeat the problem formulation and problem solving process. (6) Discuss the results, such as when the optimisation method works well, when the method does not work well. 5th Feature in 2 step 6 6.5 7 7.5 8 8.5 9 9.5 10 10.5 11 The black ellipse is used to generate the data (2D points), the green small circles are the 2D points generated, the red ellipse is the result of the optimisation problem. Problem 7. Ellipse model fitting Suppose there are N two dimensional (2D) points given in the format of (x,y) positions. Knowing the points are from the boundary of a two dimensional ellipse, find the parameters of the ellipse such that the N 2D points best fit the ellipse surface. (1) Generate the 2D points using a given ellipse; you can choose any N>20, the parameters of the ellipse; clearly describe the parameters of the ellipse and the process of how you generate the 2D points. (2) Assuming you only have the 2D points available, formulate the optimisation problem to find the parameters of the ellipse such that the fitting error is minimized; (3) Solve the problem using any optimisation method; (4) Add some small noises on the 3D points, describe how you add the noises, then use the noisy data to formulate the optimisation problem and solve the problem again. (5) Choose different parameters of the ellipse and generate the data, adding noises on the data, and repeat the problem formulation and problem solving process. (6) Discuss the results, such as when the optimisation method works well, when the method does not work well. 5th Feature in 2 step 6 6.5 7 7.5 8 8.5 9 9.5 10 10.5 11 The black ellipse is used to generate the data (2D points), the green small circles are the 2D points generated, the red ellipse is the result of the optimisation