Question: Problem #7: Let f(x) = 2, 0.7 Limn+1 (x - 2)12 n=0 7=0 7=0 00 (D) (-1) (n+ 1) OO (-1) (n+ 1) (-1) (n+




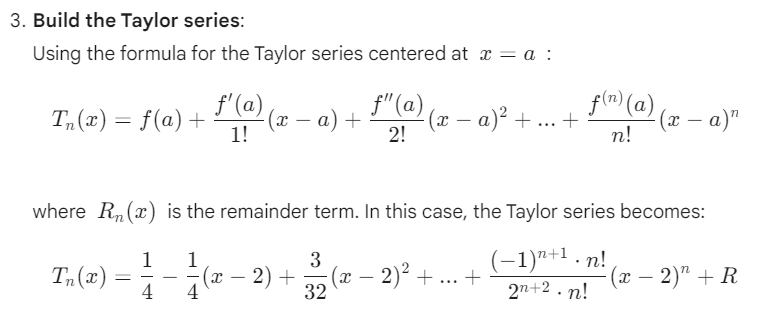

Problem #7: Let f(x) = 2, 0.7
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


