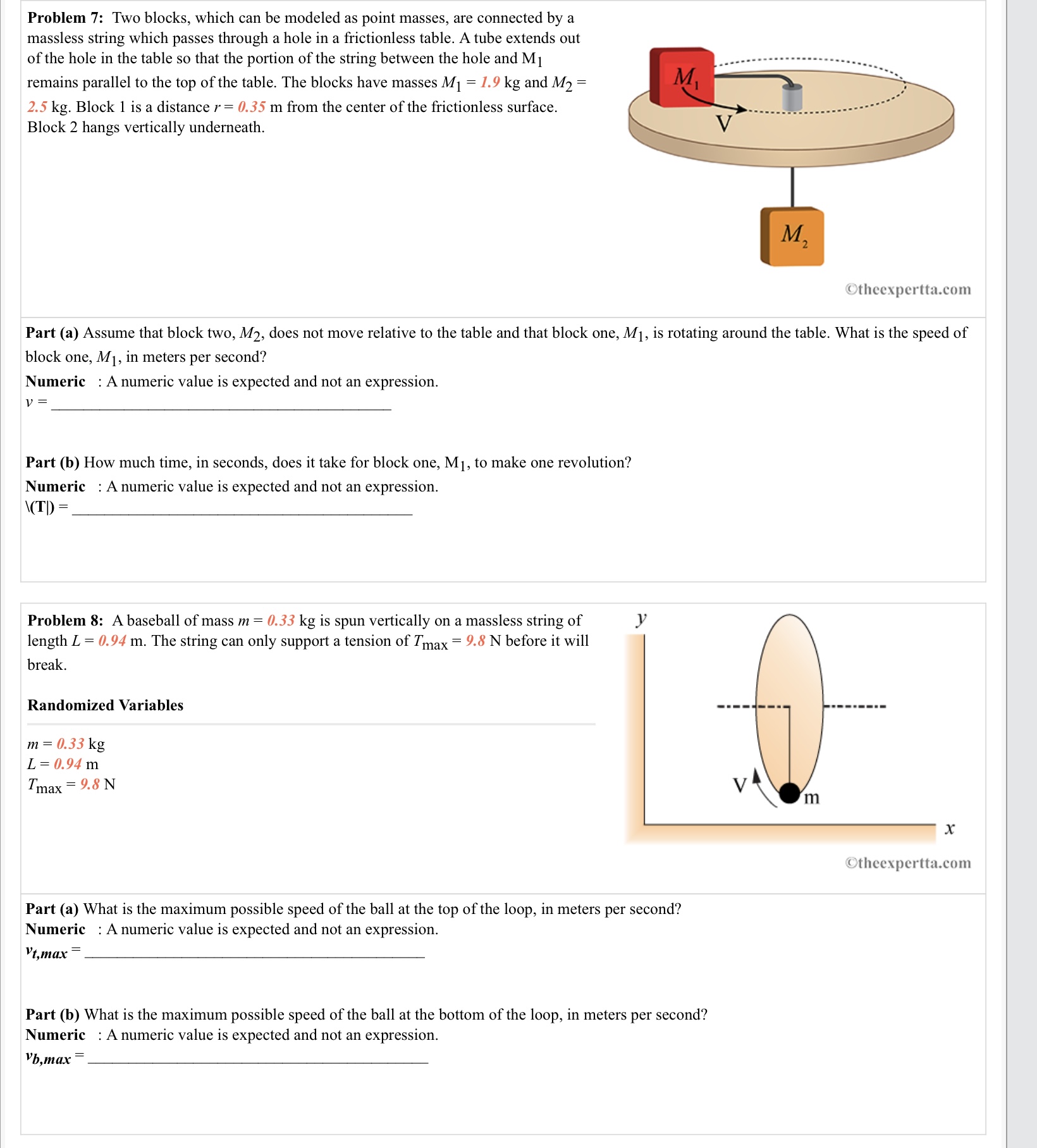
Problem 7: Two blocks, which can be modeled as point masses, are connected by a massless string which passes through a hole in a frictionless table. A tube extends out of the hole in the table so that the portion of the string between the hole and M1 remains parallel to the top of the table. The blocks have masses M1 = 1.9 kg and M2 = 2.5 kg. Block 1 is a distance r = 0.55 m from the center of the frictionless surface. Block 2 hangs vertically underneath. I lllcmpcr'lluxnm Part (a) Assume that block two, M2, does not move relative to the table and that block one, M1, is rotating around the table. What is the speed of block one, M I , in meters per second? Numeric : A numeric value is expected and not an expression. 1) : Part (b) How much time, in seconds, does it take for block one, M1, to make one revolution? Numeric .' A numeric value is expected and not an expression. \\(TI) : Problem 8: A baseball of mass m : (1.35 kg is spun vertically on a massless string of length L = (I. 94 m. The string can only support a tension of T max = 9.8 N before it will break. Randomized Variables m = 0.33 kg L = 0.94m Tmax = 9.8 N x I lhot-\\pt-r'ltaxnru Part (a) What is the maximum possible speed of the ball at the top of the loop, in meters per second? Numeric : A numeric value is expected and not an expression. \"amen: : Part (b) What is the maximum possible speed of the ball at the bottom of the loop, in meters per second? Numeric : A numeric value is expected and not an expression. vb,max =