Question: Problem 8. (1 point) The matrix A - -1 - has two real eigenvalues, one of multiplicity 1 and one of multiplicity 2. Find the

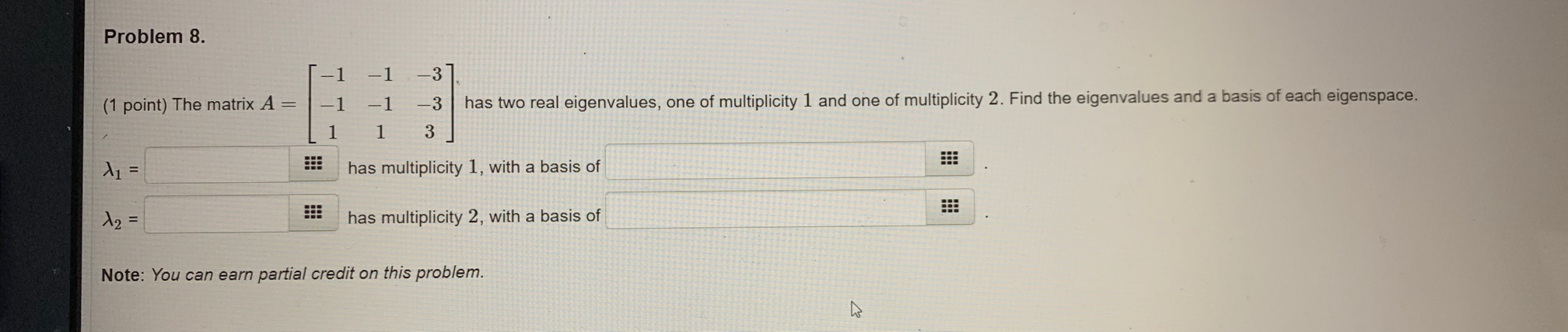
Problem 8. (1 point) The matrix A - -1 - has two real eigenvalues, one of multiplicity 1 and one of multiplicity 2. Find the eigenvalues and a basis of each eigenspace 1 1 M1= has multiplicity 1, with a basis of 12 = HE has multiplicity 2, with a basis of Note: You can earn partial credit on this problem.Problem 8. (1 point) The matrix A = -3 has two real eigenvalues, one of multiplicity 1 and one of multiplicity 2. Find the eigenvalues and a basis of each eigenspace. 3 M1= has multiplicity 1, with a basis of 12 = EEE has multiplicity 2, with a basis of Note: You can earn partial credit on this

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Line X WeBWork : 202310-MATH-122-C X + work1.cc.uregina.ca/webwork2/202310-MATH-122-C01-CO2/Assignment10/10/?key=t18N74UIWvOFTEWWCJ courses page G proquest citation -... ath-122-c01-c02 /...

Ling X WeBWork : 202310-MATH-122-C X + work].cc.uregina.ca/webwork2/202310-MATH-122-C01-CO2/Assignment10/10/?key=u0v8KOqKaNNcM60ndr4i courses page G proquest citation -... I niversity of Regina...

Ling X WeBWork : 202310-MATH-122-C X Course: MATH 122 (Petry v1): Line X WeBWork : 202310-M work1.cc.uregina.ca/webwork2/202310-MATH-122-C01-CO2/Assignment10/10/?effectiveUser=200480642&us courses...

Need an answer asap please If n is a positive integer, then Hint: Diagonalize the matrix first. Note that your answer will be a formula that involves no Be careful with parentheses. Note: You can...

Transfer |Transfer @ MP4 Cor / M Drafts (5 | My Drive | Q. ur cours |[ https://webwork1.cc.uregina.ca/webwork2/202310-MATH-122-CO1-CO2/Assignment10/10/?user=200485246&key=H5nh8.. M Gmail @ YouTube #...

(4 points) The matrix 0 2 A = 0 O has two real eigenvalues, one of multiplicity 1 and one of multiplicity 2. Find the eigenvalues and a basis for each eigenspace. The eigenvalue 1 1 is and a basis...

The matrix The eigenvalue X is A = has two real eigenvalues, one of multiplicity 1 and one of multiplicity 2. Find the eigenvalues and a basis for each eigenspace. The eigenvalue X is -2 -1 -1 0 and...

(3 points) The matrix 0 10 20 A = 0 5 10 0 5 10 has two real eigenvalues: one of multiplicity 1 and one of multiplicity 2. Find the eigenvalues and a basis for each eigenspaoe. The eigenvalue Al is...

detailed handwritten solution A=l [1 has two real eigenvalues. one of multiplicity l and one of multiplicity 2. Find the eigenvalues and a basis for each eigenspaoe. The eigenvalue A, is and a basis...

alen Trigone Mathwi sy (4x12- R Trigono Gunit cir WeBW G how to Gwhat is N Netflix New Ta G triangle...

Eight holiday lights are connected in series as shown in Fig. 5.83. a. If the set is connected to a 120-V source, what is the current through the bulbs if each bulb has an internal resistance of 28...

What is the kinetic energy per unit volume in an ideal gas at (a) P = 1.00 atm and (b) P = 300.0 atm?

Which of the following asset - backed securities does not subject the investor to credit ( default ) risk? A . Agency RMBS B . Non - Agency RMBS C . Credit caed receivable - backed securities Answer:...

2023 1040 form 1.Phillip and Claire are married and file a joint return. Phillip is self-employed as a real estate agent, and Claire is a flight attendant. Phillip and Claire have three dependent...