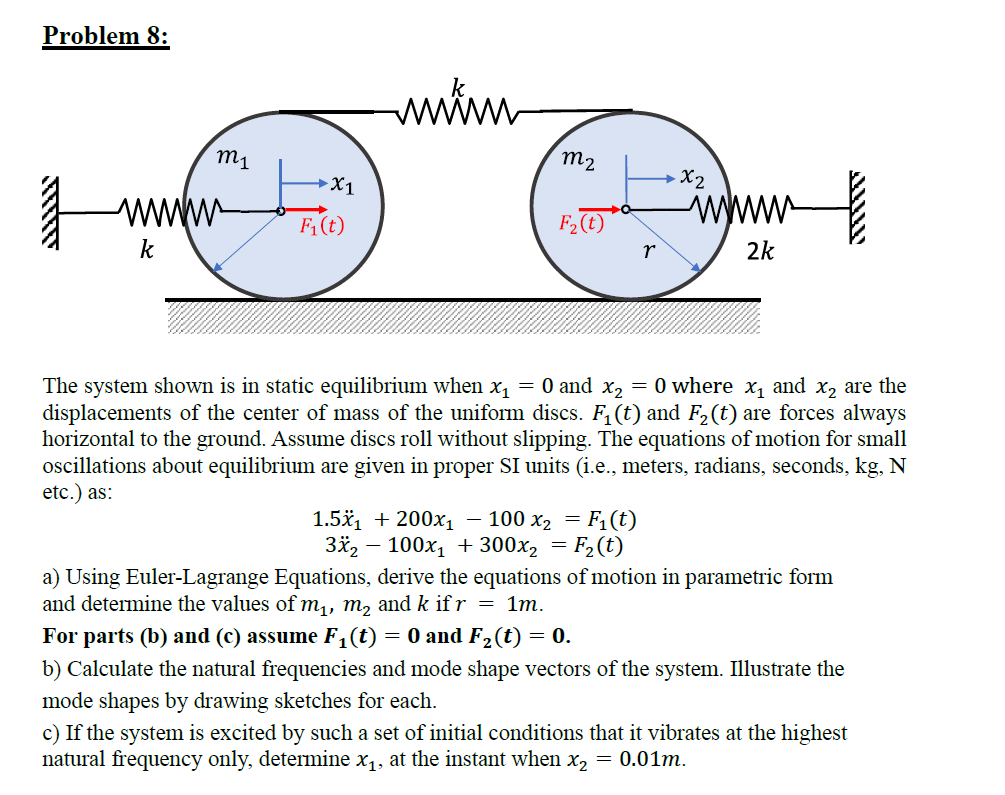
Problem $8$:

The system shown is in static equilibrium when $x_1=0$ and $x_2=0$ where $x_1$ and $x_2$ are the

displacements of the center of mass of the uniform discs. $F_1(t)$ and $F_2(t)$ are forces always

horizontal to the ground. Assume discs roll without slipping. The equations of motion for small

oscillations about equilibrium are given in proper SI units $($i$.$e$.,$ meters, radians, seconds, kg$,$ N

etc.$)$ as:

$1\mathrm{.}5x_1^{}+200x_1-100x_2=F_1(t)$

$3x_2^{}-100x_1+300x_2=F_2(t)$

a$)$ Using Euler$-$Lagrange Equations, derive the equations of motion in parametric form

and determine the values of $m_1,m_2$ and $k$ if $r=1m.$

For parts $($b$)$ and $($c$)$ assume $F_1(t)=0$ and $F_2(t)=0.$

b$)$ Calculate the natural frequencies and mode shape vectors of the system. Illustrate the

mode shapes by drawing sketches for each.

c$)$ If the system is excited by such a set of initial conditions that it vibrates at the highest

natural frequency only, determine $x_1,$ at the instant when $x_2=0\mathrm{.}01m.$