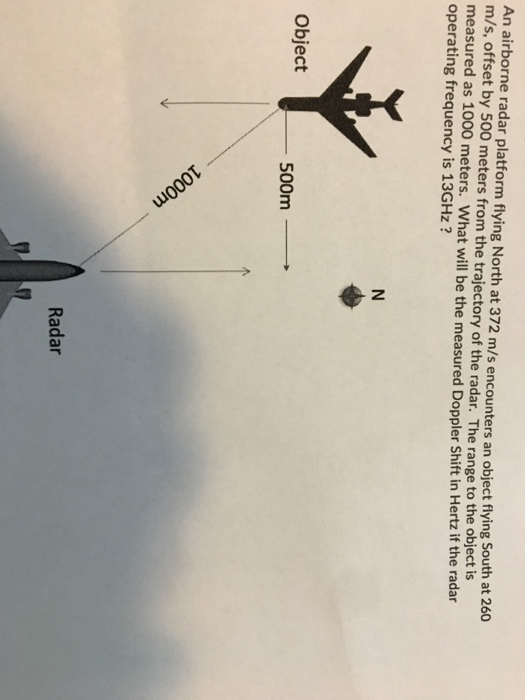
Problem 9: Consider the following non-linear systems represented by the generic form: |x| = fi (xi, X2) 2 f2(x1, x2) e f the sete . Find all equilibrium points of the non-linear system 2. Linearize the system around each equilibrium point Compute eigenvalues and eigenvectors of the linear approximation and sketch manually the qualitative behavior of the phase trajectories near the equilibrium point Sketch manually the global behavior of the system in the phase plane Does the linearized system accurately describe the local behavior of the system near the equilibrium points? Provide a MATLAB plot of the phase trajectories/velocity field (Select the plotting interval to appropriately capture the full behavior of the system) 3. 4. 5. 6. sin(x) 2 cos(x2.) 2 x2 2x2 An airborne radar platform flying North at 372 m/s encounters an object flying South at 260 m/s, offset by 500 meters from the trajectory of the radar. The range to the object is measured as 1000 meters. What will be the measured Doppler Shift in Hertz if the radar operating frequency is 13GHz? Object 500m Radar