Question: PROBLEM 9: In the MBA program at a prestigious university in the Southeastern United States, students bid for electives in the second year of their
PROBLEM 9:
In the MBA program at a prestigious university in the Southeastern United States, students bid for electives in the second year of their program. Each student has 150 points to bid (total) and must take three electives. There are four electives available: Management Science, Finance, Operations Management, and Marketing. Each class is limited to 8 students. The bids submitted for each of the 10 students are shown in the table below.
The decisions to be made in this problem are whether or not to assign each student to each class.
Formulate and solve a spreadsheet model to determine an assignment of students to classes so as to maximize the total bid points of the assignments. This is an assignment problem.
| Management | Operations | |||
| Points | Science | Finance | Management | Marketing |
| George | 70 | 20 | 20 | 40 |
| Fred | 30 | 30 | 50 | 40 |
| Ann | 55 | 55 | 15 | 25 |
| Eric | 60 | 30 | 15 | 45 |
| Susan | 40 | 40 | 40 | 30 |
| Liz | 60 | 60 | 10 | 20 |
| Ed | 80 | 30 | 20 | 20 |
| David | 35 | 35 | 45 | 35 |
| Tony | 45 | 25 | 45 | 35 |
| Jennifer | 70 | 20 | 20 | 40 |
- From your spreadsheetwhat is the total points ? (Do this in cell I29)
1500
- Solve for class assignments for each student and their bids.
3. Place the appropriate data into the model. Label your constraints appropriately.
4. You are sharing this file with a co-worker. You need to leave at least 2 comments regarding work-flow on this worksheet.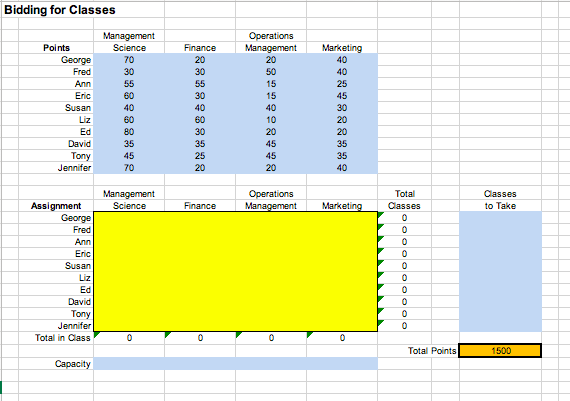
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


