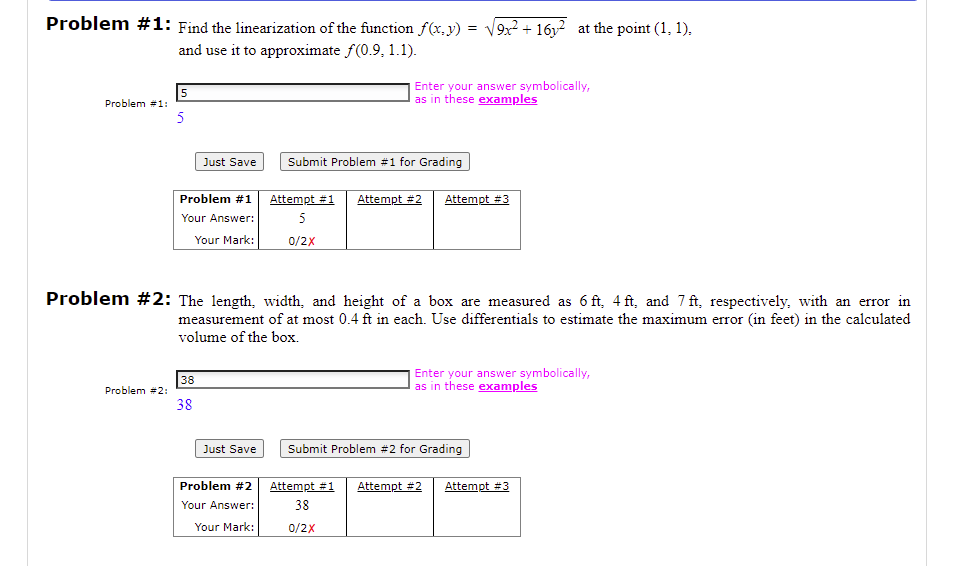
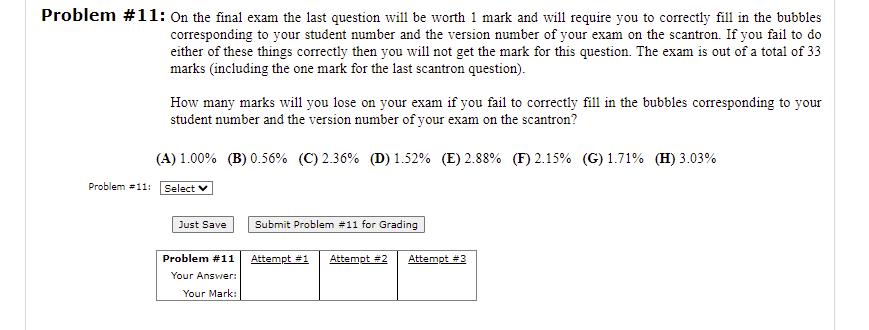
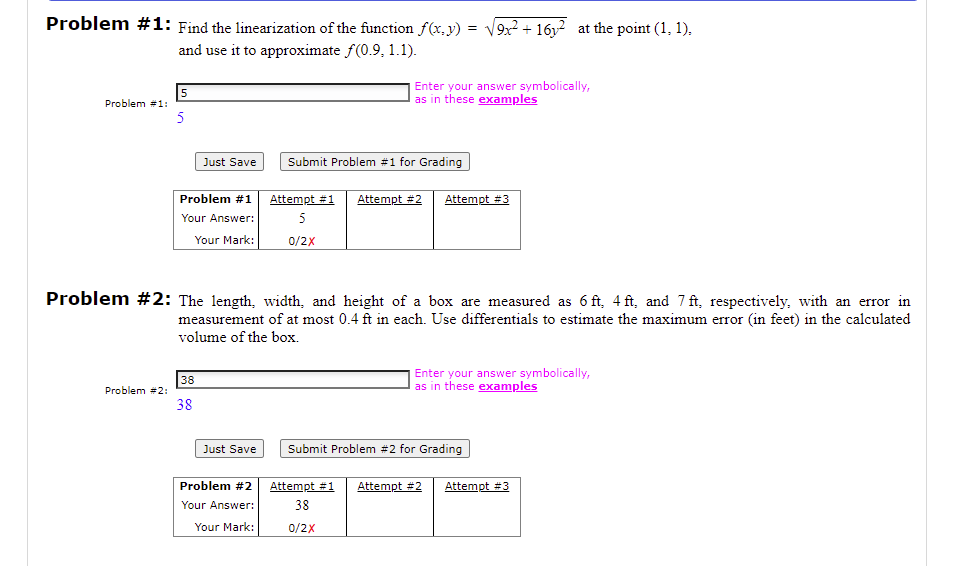
Problem #9: Let (a) Find a basis for the column space of A. (b) Find a basis for the nullspace of A. (A) {(1, 0, 0, 0). (0, 1, 0, 0)} (B) {(1, 2, 1)} (C) {(1, 2, 1). (0, 2, 0)} (D) {(1, 0, 0, 0). (0, 1, 0, 0). (0, 0, 1, 0). (0, 0, 0, 1)} (E) {(1, 2, 1). (0, 2, 0). (1, 7, 0). (1, 1, 1)} (F) {(0, 2, 0)} (G) {(1, 1, 1)} (H) {(1, 2, 1), (0, 2, 0), (1, 7, 0)} Problem =9(=): Select v (A) {(-1, ; 0, 1)} (B) {(-1, -1, 1, 0), (-1, . 0, 1)} (C) {(-1, -2, 1, 0). (-1, 2, 0, 1)} (D) {(-1, -1, 1, 0). (-1, ;. 0, 1)} (E) {(-1, 2, 0, 1)} (F) (1, ; 1, 0). (-1, } 0, 1)} (G) ((-1, 3. 0, 1)} (H) {(-1, 5 0, 1)} Problem =9(b): Select v Just Save Submit Problem #9 for Grading Problem #9 Attempt #1 Attempt #2 Attempt #3 Your Answer: 9(2) 9(=) 9(b) 9(b) Your Mark:| 9(a (E)6 9 (b) 9 (b ) 9(b) Problem #10: Let 1 6 -6 -7 -2 4 A= - 13 -5 10 (a) Find the dimension of the row space of A. (b) Find the dimension of the nullspace of A. Problem =10(=): Problem =10(b):[ Just Save Submit Problem #10 for GradingProblem #11: On the final exam the last question will be worth 1 mark and will require you to correctly ll in the bubbles corresponding to your student number and the version number of your exam on the seantron. If you fail to do either of these things correctly then you will not get the mark for this question The exam is out of a total of 33 marks (including the one mark for the last scantron question]. How many marks Twill you lose on your exam if you fail to correctly ll in the bubbles corresponding to your student number and the version number of your exam on the scantron'? {spoon (310.55% renew. {mum (15123394: mum (mum {11310393 Problem #11: Select v Just Have Submit Problem #11 For Grading Problem #11 Attempt #1 Attempt #2 Attempt #3 Your Answer: Your Mark: Problem #1: Find the linearization of the function f(x. y) = \\9x- + 16) at the point (1, 1), and use it to approximate f(0.9, 1.1). 5 Enter your answer symbolically, Problem #1: as in these examples Just Save Submit Problem #1 for Grading Problem #1 Attempt #1 Attempt #2 Attempt #3 Your Answer: 5 Your Mark: 0/2X Problem #2: The length, width, and height of a box are measured as 6 ft, 4 ft, and 7ft, respectively, with an error in measurement of at most 0.4 ft in each. Use differentials to estimate the maximum error (in feet) in the calculated volume of the box 38 Enter your answer symbolically, Problem #2: as in these examples 38 Just Save Submit Problem #2 for Grading Problem #2 Attempt #1 Attempt #2 Attempt #3 Your Answer: 38 Your Mark: 0/2XProblem #8: Let f(x, y, z) =y/*. Find the value of the following partial derivatives. (a) f(2. 2, 4) (b) f ( 2. 4. 2 ) (c) f-(3, 3, 2) Problem #8(a): (In *2)*(-4) Enter your answer symbolically, undefined variable as in these examples 'In' 2(-4) Enter your answer symbolically, Problem #8(b): as in these examples Problem #8(c): 3^(-1/3)*(In*3) Enter your answer symbolically, undefined variable as in these examples 'In' 3 -1/3.3