Problem

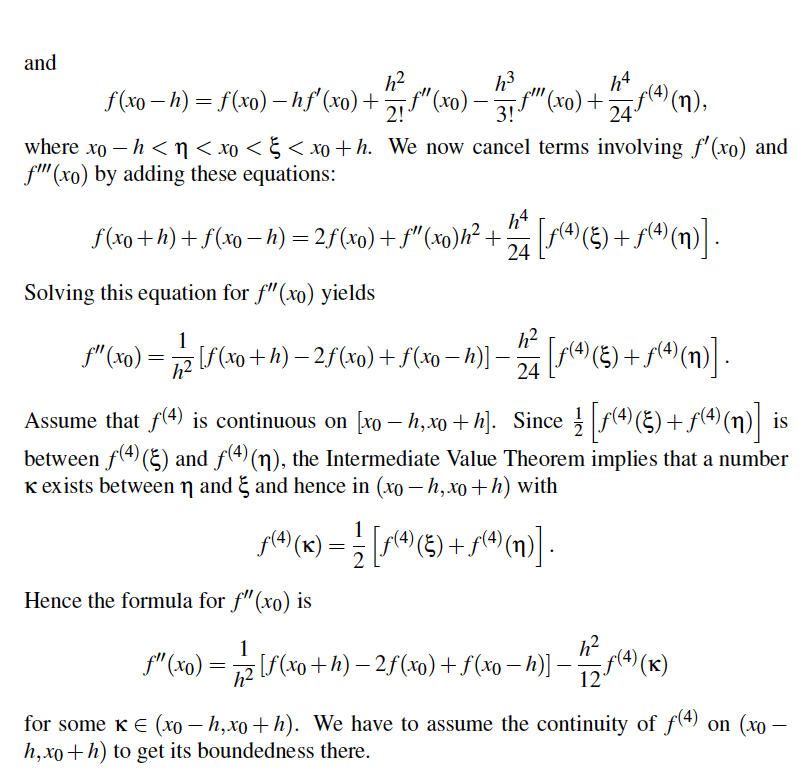
Consider a sufficiently smooth function f : R - R. Show that the follow- ing finite difference approximation of the second derivative of f is fourth order accurate: 22 f -f(x - 2h) + 16f(x - h) - 30f(x) + 16f(x th) - f(x + 2h) Or2 (x) ~ 12h21 Numerical Differentiation Recall that the derivative of the function f at xo is f'(xo) = lim (xoth) - f(xo) h -+0 h This formula gives a way of approximationg the derivative of the function f(x) at x = xo. We just compute f(xoth) - f(xo) h for a small value of h. However, we do not have any information about the quality of the approximation. In other words, we want to compute the truncation error. To this end, let f E C2 [a, b], xo,x1 E [a, b], and h = x1 -xo. To get an idea of the truncation error in approximationg f'(xo) by f(xoth) -f(xo) h we consider a Lagrange polynomial of degree 1 for the function f determined by two points xo and x 1 with its error term f (x) _ J(xO) ( x - x0 - h) f(xoth)(x-xo), (x-x0)(x-x0-h) fu(5(x)), -h h 2 for some E(x) E [a, b]. Differentiation gives f'(x) = f(roth)-f(xo) . + DX (x-xo)(x-x0-h) ,"(E(x) ) h 2 = f(xoth) - f(xo), 2(x - x0) - ham( E (x) ) +- (x -xo)(x -x0 - h2Def" (E(x)). h 2 2 If we set x = xo, we have f'(xo) = f(roth)-f(xo) h "f" ( 5 (x0 ) ) . Hence (f ( x0 ) _ f( xoth ) - f ( 0 ) 0 and backward difference formula if h