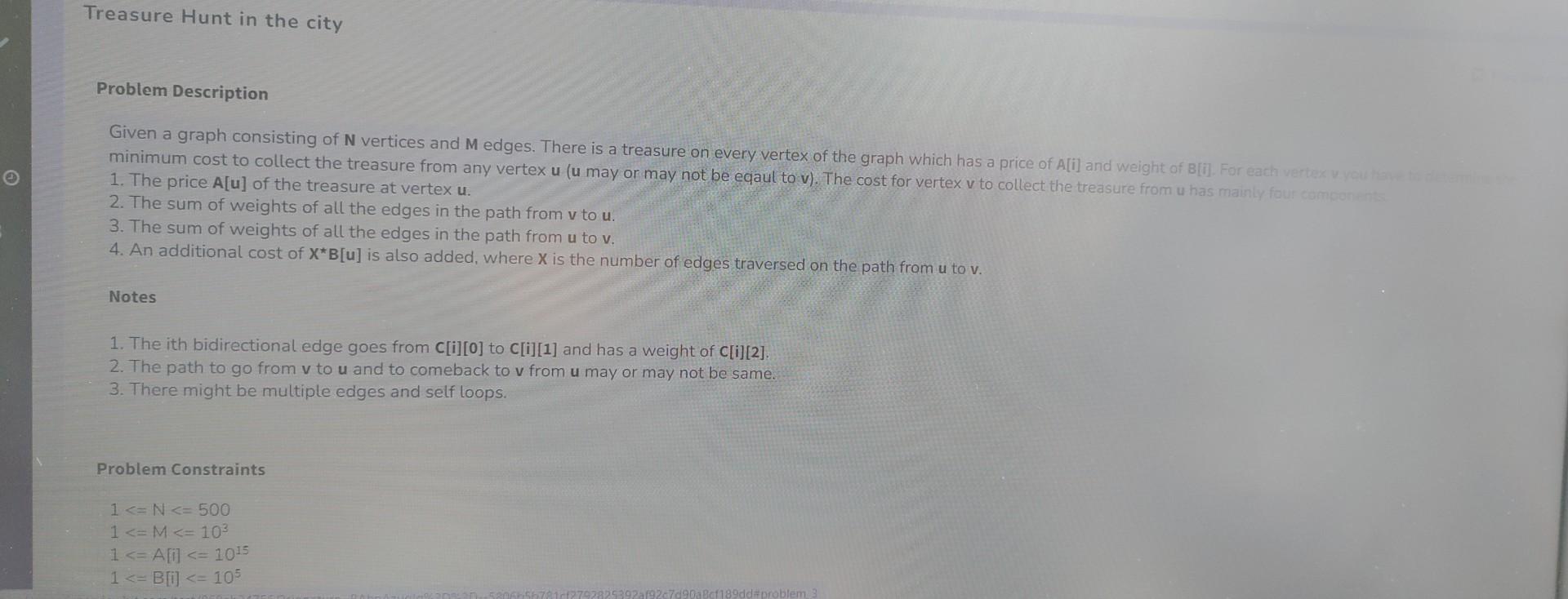
Question: Problem Description Given a graph consisting of N vertices and M edges. There is a treasure on every vertex of the graph which has a
![has a price of A[i] and weight of B[i]. For each vertex](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66efdd7062630_82366efdd6fc2777.jpg)
![v. 1. The price A[u] of the treasure at vertex u. 2.](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66efdd712d04f_82466efdd70a2cf4.jpg)
Problem Description Given a graph consisting of N vertices and M edges. There is a treasure on every vertex of the graph which has a price of A[i] and weight of B[i]. For each vertex v. 1. The price A[u] of the treasure at vertex u. 2. The sum of weights of all the edges in the path from v to u. 3. The sum of weights of all the edges in the path from u to v. 4. An additional cost of XB[u] is also added, where X is the number of edges traversed on the path from u to v. Notes 1. The ith bidirectional edge goes from C[i][0] to C[i][1] and has a weight of C[i][2]. 2. The path to go from v to u and to comeback to v from u may or may not be same. 3. There might be multiple edges and self loops. Problem Constraints 1
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


