Problem I want to solve:

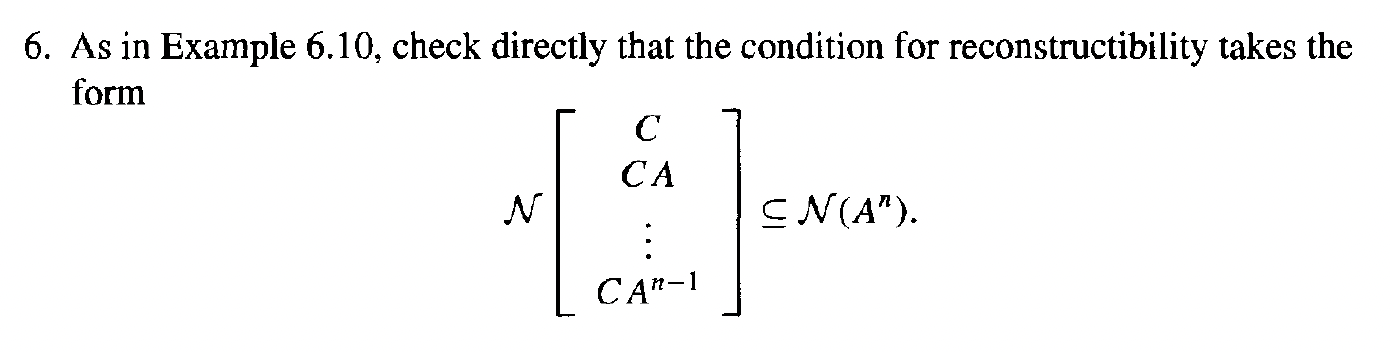
6. As in Example 6.10, check directly that the condition for reconstructibility takes the form C CA N : g N(A"). CAnl Example 6.10. We now introduce an output vector yx to the system (6.8) of Example 6.9 by appending the equation yk = CXk + Duk (6.11) with C E RPX" and D E RPXM (p 2 1). We can then pose some new questions about the overall system that are dual in the system-theoretic sense to reachability and controllability. The answers are cast in terms that are dual in the linear algebra sense as well. The condition dual to reachability is called observability: When does knowledge of fu; ) , and (yj);= suffice to determine (uniquely) xo? As a dual to controllability, we have the notion of reconstructibility: When does knowledge of {u;), , and ly; ), . suffice to determine (uniquely) x,? The fundamental duality result from linear system theory is the following: (A, B) is reachable [ controllable] if and only if ( A. B) is observable [reconstructible].To derive a condition for observability, notice that k-1 yk = CA*xo + _CAK-1-Bu; + Duk. (6.12) j=0 Thus, yo - Duo C y1 - CBuo - DuI CA XO . (6.13) Lyn-1 - 216 CA"-2-JBu; - Dun-1 - I Let v denote the (known) vector on the left-hand side of (6.13) and let R denote the matrix on the right-hand side. Then, by definition, v E R(R), so a solution exists. By the fundamental Uniqueness Theorem, Theorem 6.6, the solution is then unique if and only if N (R) = 0, or, equivalently, if and only if C CA rank = n. CAn-1