Question: Problem number 5 and tan 1 (Y/X). 5. Let U, Z be independent random variables such that U is uniform on (0, 27) and Z

Problem number 5

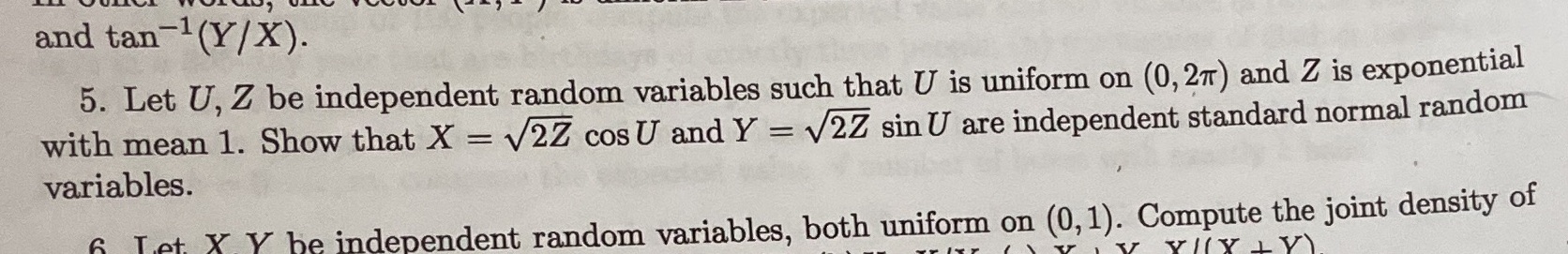
and tan 1 (Y/X). 5. Let U, Z be independent random variables such that U is uniform on (0, 27) and Z is exponential with mean 1. Show that X = v2Z cos U and Y = v2Z sin U are independent standard normal random variables. T.et Y be independent random variables, both uniform on (0, 1). Compute the joint density of YILY

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Positron Emission Tomography Image Reconstruction (Section 1.7.5 of Linear and Nonlinear Programming by Griva-Nash-Sofer, SIAM, 2009) Positron emission tomography (PET) is a medical imaging technique...

1. [-/3 Points] Indicate whether the following variables are discrete or continuous: The time it takes to cook your next dinner: continuous discrete The number of students that will register for Mat...

Problem Set due Jun 29, 2021 16:59 MST Problem 7. Sum of a random number of r.v.'s 2 points possible (graded) A fair coin is flipped independently until the first Heads is observed. Let the random...

help me please 1. Among the following distributions, the discrete distribution is (). A. B(3,0.5) B. U(0,3) C. N(0,3) D. F2,2 2. Let X,Y be two independent random variables satisfying standard normal...

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

7 Let U1 and U2 be two independent random variables, both uniformly distributed over [0, a]. Let V = min{U1, U2} and Z = max{U1, U2}. Show that the joint distribution function of V and Z is given by...

SAMPLING MEAN: DEFINITION: The term sampling mean is a statistical term used to describe the properties of statistical distributions. In statistical terms, the sample mean from a group of...

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

MUST SHOW WORK FOR PROBLEMS 40 - 50 Part A: Multiple Choice (1-16) Using the following information to answer questions 1-8: 2 _____1. a) 1.90 _____2. 1 3 0 1 2 0 5 1 4 What is the mean? b) 2.11 What...

Its macroeconomic questions could you help me solve it Question One The convolution formula is a useful trick when we are interested in the sum or average of independent random variables. In the last...

Reconsider Prob. 15-59. Using EES (or other) software, investigate the effect of the amount of excess air on the heat transfer for the combustion process. Let the excess air vary from 0 to 200...

Hispanic Business magazine publishes a list of the top 50 advertisers in the Hispanic market. The advertising spending for each of these 50 advertisers (in $ millions) was entered into a Minitab...

What is true about variance accounts? A They can be recorded with great precision so that inventories are valued with complete accuracy. B They cause a lower net income, resulting in lower income...

Axia Berhad is in the intermediate stage of a construction contract for the construction of a multiple of the telecommunication towers in several places in Malaysia . The original details of the...

The Henry, Isaac, and Jacobs partnership was about to enter liquidation with the following account balances: Estimated expenses of liquidation were $10,000. Henry, Isaac, and Jacobs shared profits...

A fish farmer has 5000 catfish in a pond. The number of catfish increases by 8% per month and the farmer harvests 420 catfish per month. a). Find a recursive equation for the catfish population Pn...

11.15 Management has stated that it will tolerate one stockout per year. The forecast of annual demand for a particular SKU is 100,000 units, and it is ordered in quantities of 10,000 units. The lead...

2. In this chapter, the reader should reflect on the following concepts: feedback and flexibility as a basis for change, intention and communication as a basis for change and behavioural patterns as...

Always have the dignity of the other or others as a backdrop.

1. There are two purposes in this chapter. The first is to break out of habits that have a limiting effect on ones own ability to change. Secondly, it is to understand how the cleaning affects the...