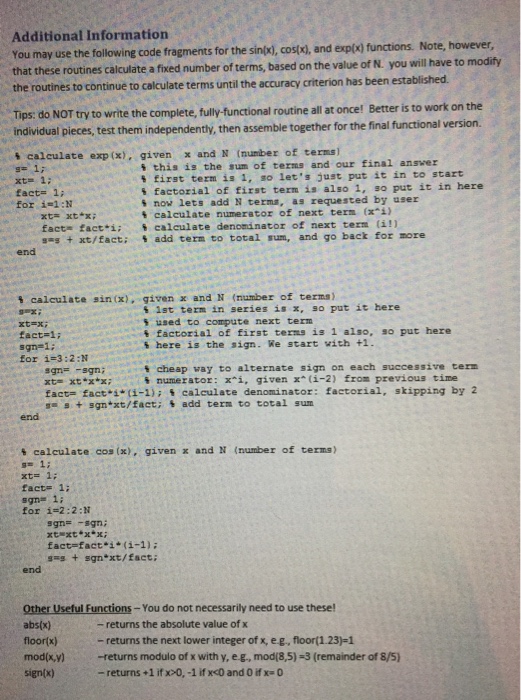
Problem overview Modify the original codes that we developed for sin(x), cos(x) and exp(x) (you can also refer to the "Additional Information") according the following design criteria: 1. (10 points) Make the calculations in the form of a callable function. Assume the argumentxis in radians 2. (10 points) Include both help document (one line) and general help in your function. 3. (90 points) For sin() and cos(x): a. Reduce the argument x, which originally can take the range of (-oo,+co) to (0, 2n) using the modulo operator (b mod (a,m) b. Further reduce the argument from part (a) to [0, r/2) using relationships for sin(x) and cos(x) in the different quadrants of the circle. c. Call a sub-function to compute the value of the new, reduced argument from (a) and (b) above. The minimum argument value will be 0 and maximum will be n/2. example if the function is called as exp(3.123), separate the 3 from the fractional component 0.123. Tip: you can use x-floor to do this. Recognizing that exp(x+y) exp(x) exp(y), compute the integer portion of the argument using a simple loop that performs the multiplication and calculate the fractional component using the series expansion. 5. (30 points) when calculating the infinite series (see Hw #3 and lecture notes of Chapter 5 for the definitions of sin, cos, and exp), continue to calculate terms until the following accuracy condition is met: a. Save the current value of the series before another term is added. Call this, for example, Soh. b. Now add the new term and calculate the new value of the summation, s w. c. Determine the absolute value of the difference between the old and new terms as d lsnew Soldl/sold. d. Stop adding terms when the absolute value of the difference between Sad and s less than a prescribed value, i.e., d E Use E 10 for all work in this assignment. built in sin, cos and exp functions in matlab