Question: Problem S2. Consider a uniform flexible chain of a fixed length L > 0 which hangs between points P = (x1, y1) and Q -

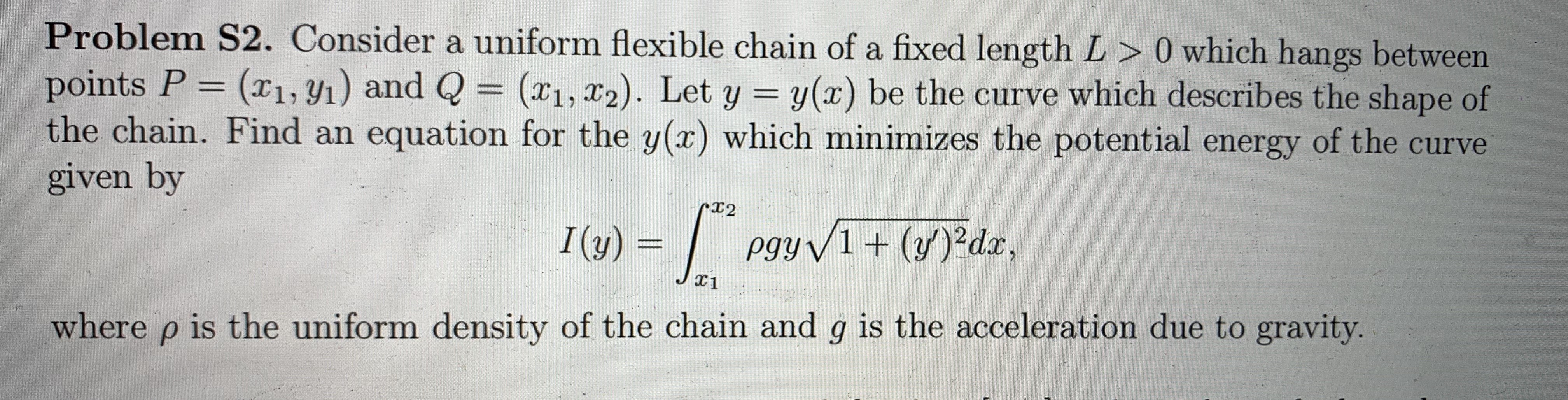
Problem S2. Consider a uniform flexible chain of a fixed length L > 0 which hangs between points P = (x1, y1) and Q - (X1, $2). Let y = y(x) be the curve which describes the shape of the chain. Find an equation for the y(x) which minimizes the potential energy of the curve given by I(y) = pgy V1 + (y')?dx, x1 where p is the uniform density of the chain and g is the acceleration due to gravity

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

If the fixed costs of manufacturing a new tablet device are $40,000, the sales price is $90, and the variable cost per unit is $50, the break-even point is

Portray in words what transforms you would have to make to your execution to some degree (a) to accomplish this and remark on the benefits and detriments of this thought.You are approached to compose...

Prolog You are approached to compose a Prolog program to work with twofold trees. Your code shouldn't depend on any library predicates and you ought to expect that the mediator is running without...

lup ] (d) Show how a generating (or "mother") wavelet (x) can spawn a family of "daughter" wavelets jk(x) by simple shifting and scaling operations, and explain the advantages of representing...

Name Student ID Final MAT 22B, Friday August 4, 2017 Instructions: This exam is closed notes, closed books, no calculators and no electronic devices of any kind. There are five problems worth 35...

Calculus 3 (Math-UA-123) Fall 2016 Homework 6 Due: Thursday, October 27 at the start of class Please give complete, well-written solutions to the following exercises. 1. Consider the function f (x,...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

HW #8 (Fault Simulation) EE 623 1. Assume you have developed an efficient table-driven event-directed logic simulation system. Consider a fan-out free circuit C having n input lines, m output line, g...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

Math 104A Homework #3 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

A company is reviewing the purchasing policy for one of its raw materials as a result of a reduction in production requirement. The material, which is used evenly throughout the year, is used in only...

Berlisle Inc. is a manufacturer of sails for small boats. The management is trying to get a better understanding of their costs and are concerned with the variances that they have seen between...

The cost formula for the maintenance department of Redwood Manufacturing is $19,500 per month plus $7.25 per machine hour used by the production department. Calculate the maintenance cost that would...

On December 31, 2020. Pina Inc. has a machine with a book value of $1,015,200. The original cost and related accumulated depreciation at this date are as follows. $1,404,000 Machine Less: Accumulated...