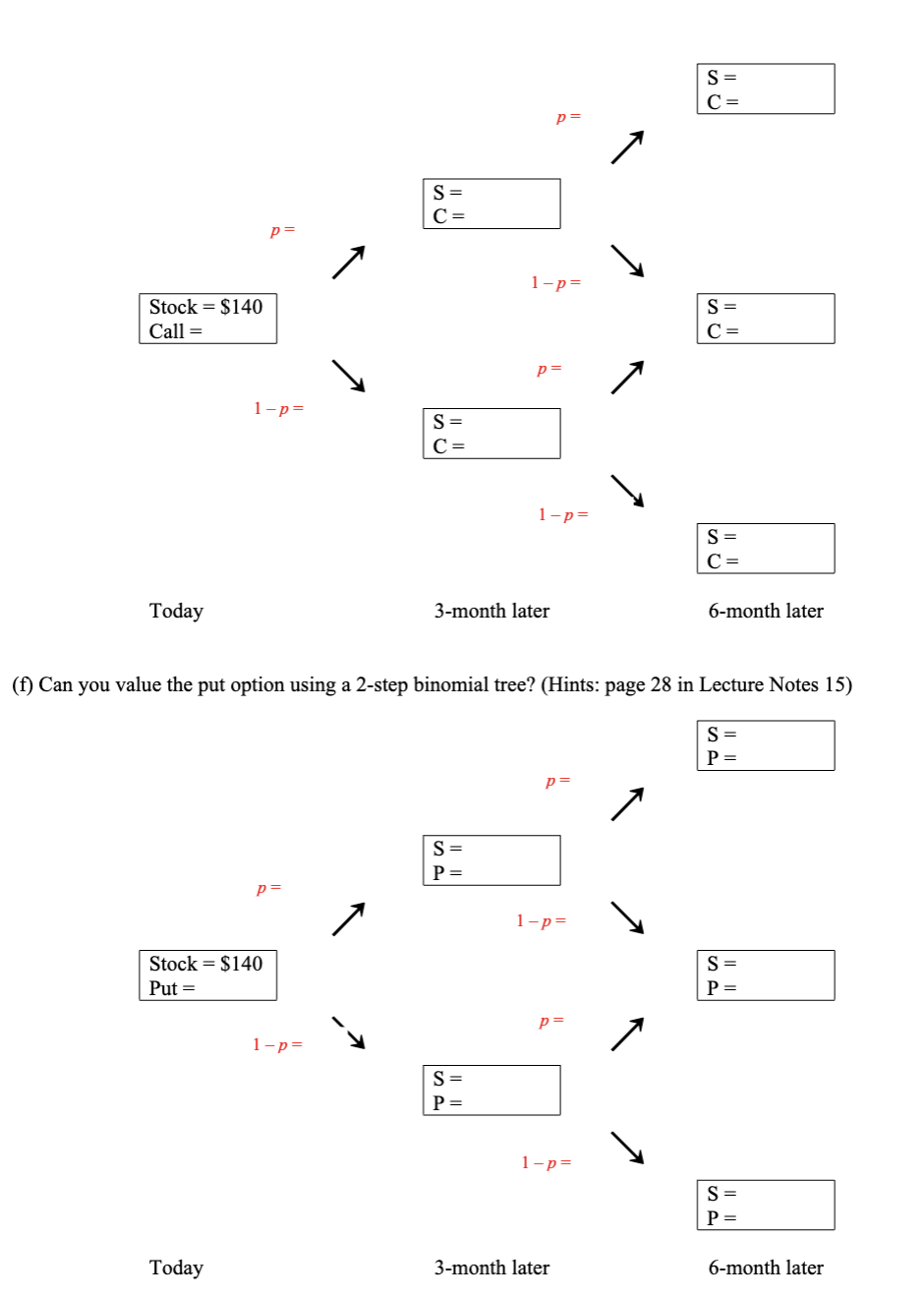
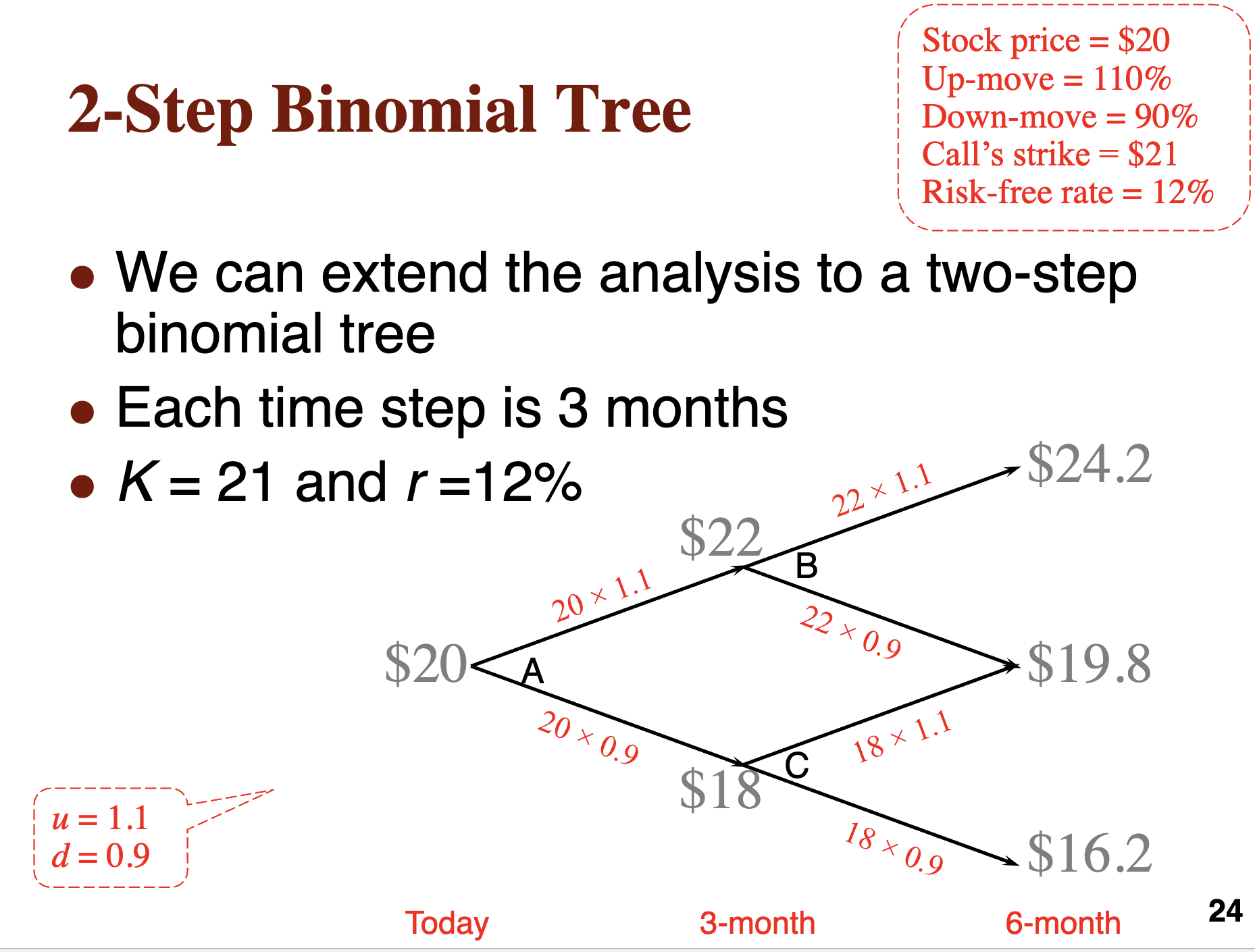
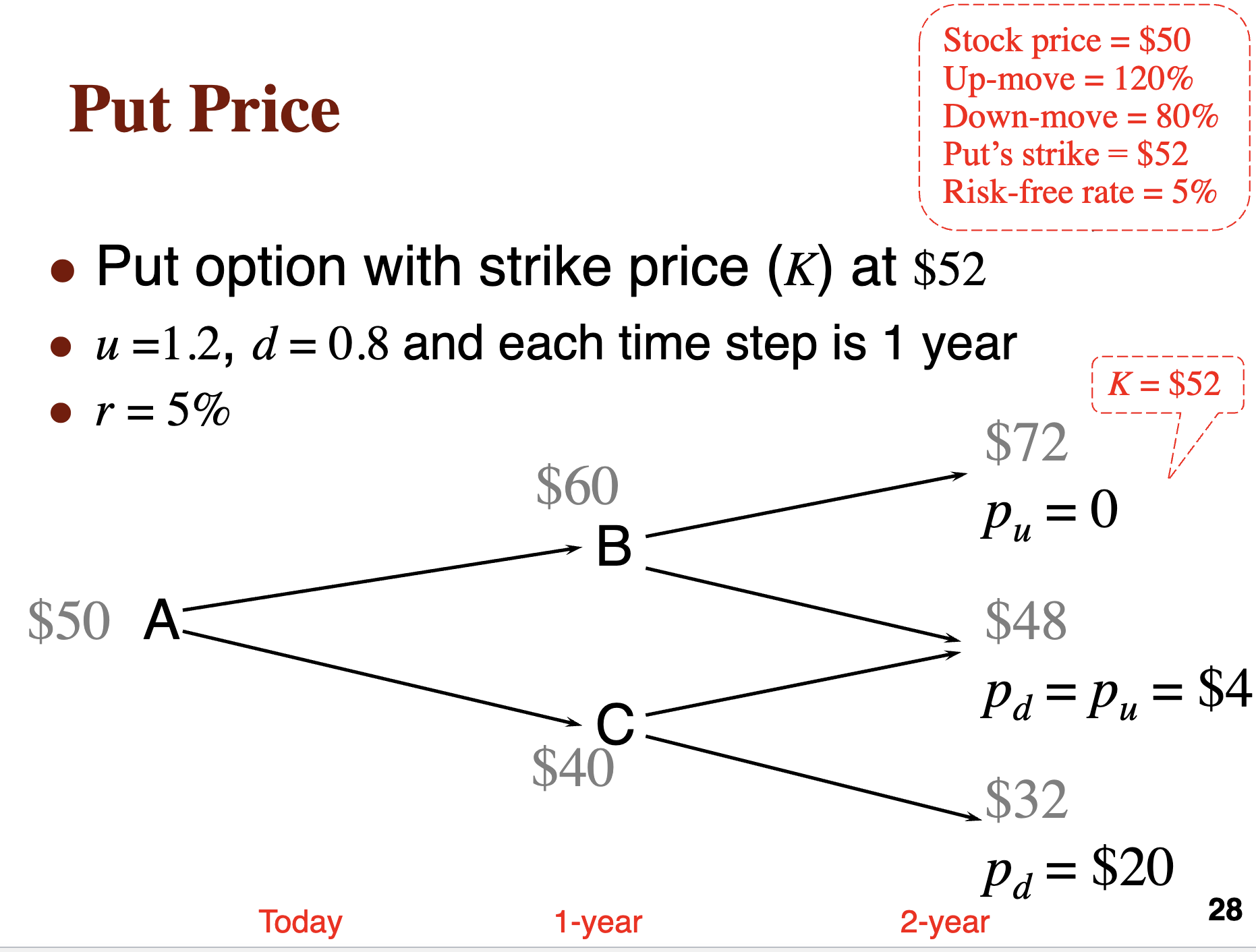
Problem Set (Chapter 12: Binomial Trees) Gilead Sciences' remdesivir (an antiviral drug) is currently undergoing clinical trials as a potential treatment for coronavirus. In this turbulent stock market, the price of Gilead's stock (GILD) looks attractive to some investors but uncertain to others. Its current price (So) is $140 and it dos not pay dividends. It has an annual volatility of 0.25 and the risk-free rate is 4%. You are considering using a straddle (long a call option and long a put option) to speculate on the stock price. Both are European options with six-month time to expiration (7) and a strike price (K) of $150. You need to set up a 2-step binomial tree to value the price for both the call and the put options. To do this, you will have to decide the size of both the up move (u) and the down move (d), and use them to calculate the risk-neutral probability (p) of the up move. Profit + $0 Loss Unlimited Profit Long Straddle Long Put Both Put and Call Strike Prices Long Call 150 Break-Even Point (Downside) Break-Even Point (Upside) Max Loss Lower Underlying Price at Expiration Higher (a) In the first step of this binomial tree, it is a 3-month period. What is the size of an up movement (u) in three months? (Hints: page 33 in Lecture Notes 15) (b) What is the size of a down movement (d) in three months? (Hints: page 33 in Lecture Notes 15) (c) What is the probability of an up movement (p) in a risk-neutral world? (Hints: page 18 in Lecture Notes 15) (d) What is the probability of a down movement in a risk-neutral world? (Hints: page 19 in Lecture Notes 15) (e) Can you value the call option using a 2-step binomial tree? (Hints: page 24 in Lecture Notes 15) 1 Stock - $140 Call Today S = C = p= 1-p= S = C= S = C = p = 1-p= S = C = p= 1-p= S = C = 3-month later 6-month later (f) Can you value the put option using a 2-step binomial tree? (Hints: page 28 in Lecture Notes 15) S = P = p= S= P p= 1-p= Stock-$140 Put = 1-p= S = P S = P = p= 1-p= S = P = Today 3-month later 6-month later How to Choose u and d In practice Page < u = d = 1/u = e 33 of 35 ZOOM + where is the annual volatility and At is the length of the time step For a 3-month-period binomial tree, At = 3/12 For a daily binomial tree, At = 1/365 or At = 1/252 Generalization of Pricing a Call Equalize these two terms (SouD - c)e-T = SD c C c = SD(1 ue) e OPTIONAL For example u = 1.1 d = 0.9 Replace D by D= Cu-cd Sou-Sod Call option price Up -rT c=e Down [pc+(1-p)ca] erT -d where p: u-d What is p? Probability? 18 OPTIONAL p as a Probability for Risk-Free Return It is natural to interpret p and 1-p as the probabilities of up and down movements Today So P Sou Time T = 7461A 7%% TREASURY BOND OF 2002-2007 Dated February 15, 1977 Due February 15, 2007 CUSIP 912810 BX 5 Redeemable on calls and after February 15, 2002 CIRCULAR No. 4-77 THE UNITED STATES OF AMERICA FOR VALUE RECEIVED PROMISES TO PAY TO THE BEARER THE SUM OF ONE THOUSAND DOLLARS (1 - p) Sod When the probability of an up and down movements are p and 1-p, the expected stock price at time T is SperT 19 2-Step Binomial Tree Stock price = $20 Up-move 110% = Down-move = 90% Call's strike = $21 Risk-free rate = 12% We can extend the analysis to a two-step . binomial tree Each time step is 3 months K= 21 and r=12% 22 x 1.1 $24.2 $22 B 22 0.9 $20A 20 x 1.1 20 0.9 $18 C 18 x 1.1 $19.8 u = 1.1 d = 0.9 Today 3-month 18 0.9 $16.2 24 6-month Put Price Stock price = $50 Up-move =120% Down-move = 80% Put's strike = $52 Risk-free rate = 5% Put option with strike price (K) at $52 u =1.2, d=0.8 and each time step is 1 year r = 5% $50 A: $60 B $40 $72 Pu = 0 $48 K = $52 Pa = P = $4 Pu Pd $32 Pd = $20 Today 1-year 28 2-year