Problem Statement

We encounter projectile motion whenever we attempt to catch a fly ball, hit a long drive, or shoot a free throw. The laws of physics, which describe projectile motion, are well known. They were first studied by Napoleons generals.

To simplify the problem, we will assume that we can

- consider the surface of the Earth to be a plane

- ignore the effect of the drag from air friction

Under the simplifying conditions above, the following formulas hold for a projectile with an initial velocity of v feet/sec and a launch angle of r (note that these expressions are not written according to the syntax of the Java language).

1. Time span of the flight: T = 2 v sin r / g

2. Maximum height: y_max = (v sin r) t - g t, where t = T/2

3. Range (distance traveled by the projectile): x_max = (v cos r) T

Here g is the gravitational acceleration g = 32 ft/sec² (in English units) and r is measured in radians.

This project simulates the process of repeated attempts to hit a target with a projectile. The goal is to shoot the projectile within a 1-foot distance from the target, since such a short miss is accepted as a hit. You will construct a Java program that

• can determine the trajectory data of a projectile for a given initial velocity and a launch angle, in particular for an initial choice of a 45-degree angle;
• can check if the initial attempt overshoots the target with more than 1 foot; if so the process is terminated and then restarted with an increased initial velocity (note that for any initial velocity the longest range is attained if the launch angle is of 45 degrees);
• can determine the error of a shot (error = projectile range distance to target);
• can check if the error is less than 1 foot in absolute value; if so, the user is notified about the result and the process terminates;
• can offer the user four chances to modify the launch angle and try to hit the target;
• can keep track of the smallest error produced by the subsequent attempts; the best result is reported to the user.

Analysis and requirements

The analysis describes the logical structure of the problem in a way which helps us to plan (design) a solution.

Input

Initial input values are

(i) initial velocity (feet/sec),

(ii) distance to the desired target (feet), and

(iii) the gravitational acceleration (a constant).

Additional input values are the launch angles for the repeated attempts if applicable. The angle must always be in the range of 0.0 45.0 degrees.

Distance, velocity and launch angle are solicited from the user on JOptionPane input windows. See Figures 1, 2, 3.

Output

Output messages are displayed both on JOptionPane windows and on the console. Every time a launch has been executed by the program, a report providing the details of the trajectory must be displayed as shown on Figure 4.

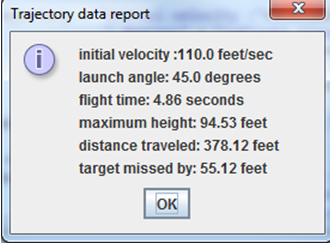
Each report must contain

1. the initial velocity in feet/sec,
2. the current launch angle in degrees,
3. the flight time in seconds,
4. the maximum height attained,
5. the distance traveled by the projectile (range), and
6. the error with which the projectile missed the target.

Note that the error is a positive value when the projectile overshoots, and negative for short shots. All real numbers displayed must be rounded to the nearest hundredth.

The first report is based upon launch angle of 45 degrees (which provides the longest possible range) to see if the target is within reach at all for the given velocity. If the first attempt falls short of the target, another window as shown on Figure 5 displays the information and then the program exits.

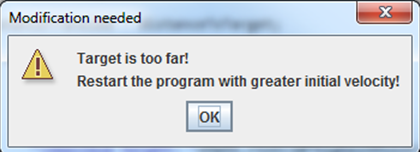
Figure 7 shows a sample output using Joptionpane

Shot went beyond the target. Decrease the launch angle!

Shot went beyond the target. Decrease the launch angle!

Shot fell short of the target. Increase the launch angle!

Shot went beyond the target. Decrease the launch angle!

Shot fell short of the target. Increase the launch angle!

Your best shot missed the target with 2.76 feet.

Figure 7

Note that it is necessary to keep track of the least absolute error occurred in the series of attempts, since it has to be reported as the last line in Figure 7 shows.

Figure 8 shows a successful launch. Such a report is followed by the message of Figure 9.

figure 8

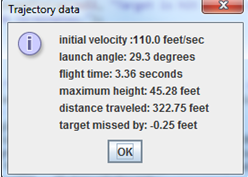
figure 9

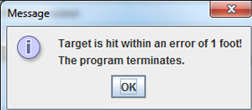
Input x ? Enter distance to target in feet: 323 OK Cancel Input x ? Enter initial velocity in feet/sec: 110 OK Cancel X Input ? Enter the launch angle in degrees: 45 OK Cancel x Trajectory data report i initial velocity: 110.0 feet/sec launch angle: 45.0 degrees flight time: 4.86 seconds maximum height: 94.53 feet distance traveled: 378.12 feet target missed by: 55.12 feet OK Modification needed x Target is too far! Restart the program with greater initial velocity! OK Trajectory data i initial velocity :110.0 feet/sec launch angle: 29.3 degrees flight time: 3.36 seconds maximum height: 45.28 feet distance traveled: 322.75 feet target missed by: -0.25 feet OK Message x i Target is hit within an error of 1 foot! The program terminates. OK