Problem Title: Sum of Subsets Using Backtracking

Problem Description: Given a sum of subsets problem where W$=7$ and w$=[2,3,4,5],$ solve this problem using the backtracking method to find all possible solutions. When following the pseudocode below, you need to determine:

The total number of nodes generated in the state space tree during the execution of the algorithm

The number of solutions found when executing this backtracking approach

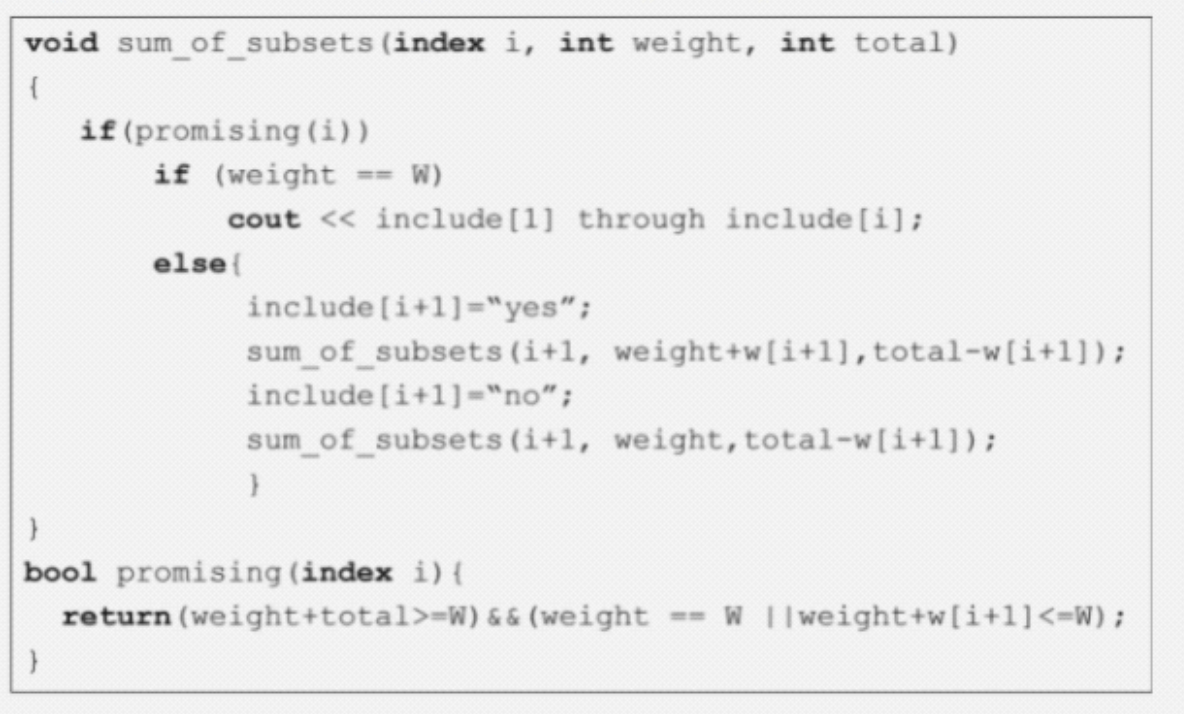
The following code implements the sum of subsets algorithm:

void sum$\_$of$\_$subsets$($index i$,$ int weight, int total$)\{$ if$($promising$($i$))$ if $($weight $==$ W$)$ cout $$ include$[1]$ through include$[$i$]$; else$\{$ include$[$i$+1]=$"yes"; sum$\_$of$\_$subsets$($i$+1,$ weight$+$w$[$i$+1],$total$-$w$[$i$+1])$; include$[$i$+1]="$no$"$; sum$\_$of$\_$subsets$($i$+1,$ weight,total$-$w$[$i$+1])$; $\}\}$ bool promising$($index i$)\{$ return$($weight$+$total$>=$W$)$&&$($weight $==$ W $||$weight$+$w$[$iW$)$; $\}$

Note that during the execution of sum$\_$of$\_$subsets, we define that one node is generated each time we make a decision about including or excluding an element.

Questions to answer:

Total number of nodes $=\_\_\_\_\_\_\_$

Number of solutions $=\_\_\_\_\_\_\_$

Additional Context:

The problem uses backtracking to find all possible combinations of the given weights that sum to the target value W

The promising function is used to determine whether a partial solution is worth exploring further

Each node in the state space tree represents a decision point in the algorithm

Please provide your answers with detailed explanations showing your reasoning process. $```$

void sum$\_$of$\_$subsets$($index i$,$ int weight, int total$)$

$\{$

if$($promising$($i$))$

if $($weight $==$ W$)$

cout $$ include$[1]$ through include$[$i$]$;

else$\{$

include$[$i$+1]=$"yes";

sum$\_$of$\_$subsets$($i$+1,$ weight$+$w$[$i$+1],$total$-$w$[$i$+1])$;

include $[$i$+1]="$no$"$;

sum$\_$of$\_$subsets$($i$+1,$ weight,total$-$w$[$i$+1])$;

$\}$

$\}$

bool promising$($index i$)\{$

return$($weight$+$total$>=$W$)$ &&$($weight $==$ W $||$weight$+$w$[$iW$)$;

$\}$

$```$